题目内容
5. 如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.连接DE,则DF的长是( )
如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.连接DE,则DF的长是( )| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{7}{8}$ | D. | $\frac{25}{8}$ |
分析 由四边形ABCD是矩形与△AEC由△ABC翻折得到,AD=CE,∠ADF=∠CEF,由AAS证得△ADF≌△CEF,的长FA=FC,设DF=x,则FA=4-x,由勾股定理得:DA2+DF2=AF2,即可求出DF的长.
解答 解:∵四边形ABCD是矩形,
∴AD=BC,AB=DC=4,∠ADF=90°,∵△AEC由△ABC翻折得到,
∴BC=EC,∠CEF=∠ABC=90°,
∴AD=CE,∠ADF=∠CEF,
在△ADF与△CEF中,
$\left\{\begin{array}{l}{∠ADF=∠CEF}\\{∠AFD=∠CFE}\\{AD=CE}\end{array}\right.$,
∴△ADF≌△CEF(AAS),
∴FA=FC,
设DF=x,则FA=FC=DC-DF=4-x,
在Rt△DFA中,由勾股定理得:DA2+DF2=AF2,
即32+x2=(4-x)2,
解得:x=$\frac{7}{8}$,
即DF的长是$\frac{7}{8}$.
故选C.
点评 本题主要考查了折叠的性质、矩形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握折叠的性质,得到相等的线段与角是解决问题的关键.

练习册系列答案
相关题目
10. 已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )
已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )
 已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )
已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )| A. | k1=$\frac{1}{4}$,k2=4 | B. | k1=4,k2=$\frac{1}{4}$ | C. | k1=$\frac{1}{4}$,k2=-4 | D. | k1=-$\frac{1}{4}$,k2=4 |
 如图,AB∥CD,∠A=110°,CE平分∠ACD,则∠ECD=35°.
如图,AB∥CD,∠A=110°,CE平分∠ACD,则∠ECD=35°. 如图,是一个包装盒的三视图,则这个包装盒的表面积是600πcm2(结果保留π)
如图,是一个包装盒的三视图,则这个包装盒的表面积是600πcm2(结果保留π)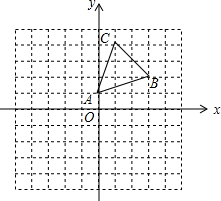 如图,△ABC的顶点均在正方形网格的格点上,在已知的直角坐标系中,A(0,1),B(3,2).
如图,△ABC的顶点均在正方形网格的格点上,在已知的直角坐标系中,A(0,1),B(3,2). (1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长度.
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长度.