题目内容
17．抛物线y=ax2+bx+c开口向上，其对称轴为直线x=1，若其与x轴一交点为B（3，0），则当ax2+bx+c＞0时，x的取值范围是x＜1或x＞3．分析 首先求得B关于x=1的对称点，然后结合函数开口向上，即可直接写出不等式的解集．
解答 解：B关于x=1的对称点是（1，0）．
又∵抛物线y=ax2+bx+c开口向上，
∴ax2+bx+c＞0时，x的取值范围是x＜1或x＞3．
故答案是：x＜1或x＞3．
点评 本题考查了二次函数的图象与不等式的解集的关系，根据对称轴求得二次函数与x轴的交点坐标是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在△ABC中，AB=AC，BD是AC边上的高，若∠A=40°，则∠DBC的大小为20度．
5．
如图，四边形ABCD是矩形，AB=4，AD=3，把矩形沿直线AC折叠，点B落在点E处，AE交CD于点F．连接DE，则DF的长是（ ）
如图，四边形ABCD是矩形，AB=4，AD=3，把矩形沿直线AC折叠，点B落在点E处，AE交CD于点F．连接DE，则DF的长是（ ）| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | $\frac{7}{8}$ | D． | $\frac{25}{8}$ |
如图，在平面直角坐标系中，小正方形网格边长为1．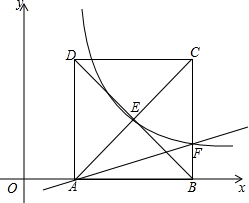
如图，正方形ABCD顶点C的坐标为（5，4），顶点A在x轴的正半轴上，反比例函数y=$\frac{k}{x}$的图象经过AC与BD的交点E，与边BC交于点F．
7．
如图是某几何体从三个不同方向看得到的平面图形，则这个几何体是（ ）
如图是某几何体从三个不同方向看得到的平面图形，则这个几何体是（ ）| A． | 长方体 | B． | 圆锥 | C． | 圆柱 | D． | 球 |