题目内容
4. 如图,在△ABC中,AC=8,AB=10,∠BAC=60°,⊙O与AB,AC都相切,与AB的切点为E.
如图,在△ABC中,AC=8,AB=10,∠BAC=60°,⊙O与AB,AC都相切,与AB的切点为E.(1)求⊙O的面积y关于EA的长x的函数表达式.
(2)当⊙O为△ABC的内切圆时,求x和y的值.
(3)P是⊙O上的动点,以AP为半径的⊙P分别交AB,AC于点F,G,连结FG.若EA=$\sqrt{3}$,求FG的最大值和最小值.
分析 (1)如图1,连接AO,OE,在Rt△AOE中,求出OE(用x的代数式表示),然后利用圆面积公式即可解决问题.
(2)如图2中,作CM⊥AB于M.首先求出BC,设AC,BC分别切⊙O于点F,G,由⊙O为△ABC的内切圆,设AF=AE=x,设CF=CG=a,BE=BG=b,列出方程组求解即可.
(3)如图3中,连接AO交⊙O于P,延长AO交⊙O于P1,①当⊙P 的半径为AP时,GF的值最小,②当⊙P 的半径为AP1时,G1F1的值最大,由①可知△G1F1A是等边三角形,利用△AFG是等边三角形即可解决问题.
解答 解:(1)如图1,连接AO,OE,
∵⊙O与AB,AC都相切,∠BAC=60°,
∴∠OAE=30°,
∴OE=$\frac{\sqrt{3}}{3}$AE=$\frac{\sqrt{3}}{3}$x,
∵y=($\frac{\sqrt{3}}{3}$x)2π=$\frac{π}{3}$x2;
(2)如图2中,作CM⊥AB于M.
在Rt△ACM中,∵∠CAM=60°,AC=8,∠AMC=90°,
∴∠ACM=30°,AM=$\frac{1}{2}$AC=4,BM=AB-AM=6,CM=4$\sqrt{3}$,
∴BC=$\sqrt{C{M}^{2}+B{M}^{2}}$=$\sqrt{(4\sqrt{3})^{2}+{6}^{2}}$=2$\sqrt{21}$,
设AC,BC分别切⊙O于点F,G,
∵⊙O为△ABC的内切圆,
∴AF=AE=x,设CF=CG=a,BE=BG=b,
∴$\left\{\begin{array}{l}{x+a=8}\\{x+b=10}\\{a+b=2\sqrt{21}}\end{array}\right.$,
∴x=9-$\sqrt{21}$,
∴y=34π-6$\sqrt{21}$π;
(3)如图3中,连接AO交⊙O于P,延长AO交⊙O于P1,
①当⊙P 的半径为AP时,GF的值最小,
∵∠CAB=60°,OE⊥AE,
∴∠OAB=∠OAC=30°,
∴AO=2OE,
∴AP=OP=PG=PF,
∴E、F重合,
∴AP垂直平分GF,
∴AG=AF,∵∠GAF=60°,
∴△AGF是等边三角形,
∵AE=$\sqrt{3}$,
∴AE=AG=GF=$\sqrt{3}$,
∴FG的最小值为$\sqrt{3}$.
②当⊙P 的半径为AP1时,G1F1的值最大,由①可知△G1F1A是等边三角形,
∵AP1=P1G1=P1F1=3,
∴G1F1=$\frac{3\sqrt{3}}{2}$,
∴FG的最大值为$\frac{3\sqrt{3}}{2}$.
点评 本题考查圆综合题、切线长定理、直角三角形30度角性质、等边三角形的判定和性质、三元一次方程组等知识,解题的关键是灵活应用所学知识解决问题,学会添加辅助线,构造直角三角形,学会利用特殊点解决最值问题,属于中考压轴题.

| A. | 图象必经过点(1,2) | B. | y的值随x值的增大而减小 | ||
| C. | 图象在第一、三象限内 | D. | 若x>1,则0<y<2 |

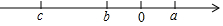 已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
 如图,四边形ABCD内接于⊙O,E为CD延长线上一点,若∠B=96°,则∠ADE的度数为96度.
如图,四边形ABCD内接于⊙O,E为CD延长线上一点,若∠B=96°,则∠ADE的度数为96度.