题目内容
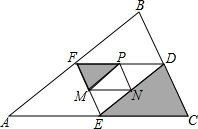 如图,△ABC三边的中点D,E,F组成△DEF,△DEF三边的中点M,N,P组成△MNP,将△FPM与△ECD涂成阴影.假设可以随意在△ABC中取点,那么这个点取在阴影部分的概率为
如图,△ABC三边的中点D,E,F组成△DEF,△DEF三边的中点M,N,P组成△MNP,将△FPM与△ECD涂成阴影.假设可以随意在△ABC中取点,那么这个点取在阴影部分的概率为考点:三角形中位线定理,几何概率
专题:几何图形问题
分析:先设阴影部分的面积是x,得出整个图形的面积,再根据几何概率的求法即可得出答案.
解答:解:∵D、E分别是BC、AC的中点,
∴DE是△ABC的中位线,
∴ED∥AB,且DE=
AB,
∴△CDE∽△CBA,
∴
=(
)2=
,
∴S△CDE=
S△CBA.
同理,S△FPM=
S△FDE=
S△CBA.
∴S△FPM+S△CDE=
S△CBA.
则
=
.
故答案是:
.
∴DE是△ABC的中位线,
∴ED∥AB,且DE=
| 1 |
| 2 |
∴△CDE∽△CBA,
∴
| S△CDE |
| S△CBA |
| ED |
| AB |
| 1 |
| 4 |
∴S△CDE=
| 1 |
| 4 |
同理,S△FPM=
| 1 |
| 4 |
| 1 |
| 16 |
∴S△FPM+S△CDE=
| 5 |
| 16 |
则
| S阴影 |
| S△CBA |
| 5 |
| 16 |
故答案是:
| 5 |
| 16 |
点评:本题考查了三角形中位线定理和几何概率.几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
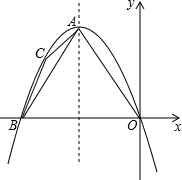 如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=-2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为
如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=-2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为 如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是
如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是 如图,△ABC中,∠C=90°,AB垂直平分线交BC于D.若BC=8,AD=5,则AC等于
如图,△ABC中,∠C=90°,AB垂直平分线交BC于D.若BC=8,AD=5,则AC等于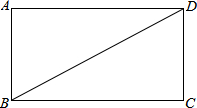 如图,BD是矩形ABCD的一条对角线.
如图,BD是矩形ABCD的一条对角线.