题目内容
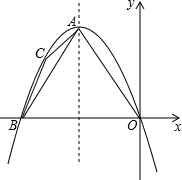 如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=-2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为
如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=-2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为考点:二次函数的性质
专题:计算题
分析:根据抛物线的对称性得到:OB=4,AB=AO,则四边形AOBC的周长为AO+AC+BC+OB=△ABC的周长+OB.
解答:解:如图,∵对称轴为直线x=-2,抛物线经过原点、x轴负半轴交于点B,
∴OB=4,
∵由抛物线的对称性知AB=AO,
∴四边形AOBC的周长为AO+AC+BC+OB=△ABC的周长+OB=a+4.
故答案为:a+4.
∴OB=4,
∵由抛物线的对称性知AB=AO,
∴四边形AOBC的周长为AO+AC+BC+OB=△ABC的周长+OB=a+4.
故答案为:a+4.
点评:本题考查了二次函数的性质.此题利用了抛物线的对称性,解题的技巧性在于把求四边形AOBC的周长转化为求(△ABC的周长+OB)是值.

练习册系列答案
相关题目
 如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,求证:四边形ABCD是菱形.
如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,求证:四边形ABCD是菱形. 根据如图所给信息,回答下列问题:
根据如图所给信息,回答下列问题:
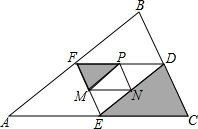 如图,△ABC三边的中点D,E,F组成△DEF,△DEF三边的中点M,N,P组成△MNP,将△FPM与△ECD涂成阴影.假设可以随意在△ABC中取点,那么这个点取在阴影部分的概率为
如图,△ABC三边的中点D,E,F组成△DEF,△DEF三边的中点M,N,P组成△MNP,将△FPM与△ECD涂成阴影.假设可以随意在△ABC中取点,那么这个点取在阴影部分的概率为