题目内容
20.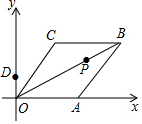 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )| A. | (1,$\frac{1}{2}$) | B. | ($\frac{4}{3}$,$\frac{2}{3}$) | C. | ($\frac{6}{5}$,$\frac{3}{5}$) | D. | ($\frac{10}{7}$,$\frac{5}{7}$) |
分析 如图,连接AC交OB于K,作KH⊥OA于H.由四边形ABCD 是菱形,推出AC⊥OB,A、C关于对角线OB对称,推出PC=PC,推出PC+PD=PA+PD,所以当D、P、A共线时,PC+PD的值最小,求出直线OB与直线AD的交点即可解决问题.
解答 解:如图,连接AC交OB于K,作KH⊥OA于H.
∵四边形ABCD 是菱形,
∴AC⊥OB,A、C关于对角线OB对称,
∴PC=PC,
∴PC+PD=PA+PD,
∴当D、P、A共线时,PC+PD的值最小,
在Rt△OAK中,∵OK=2$\sqrt{5}$,OA=5,
∴AK=$\sqrt{O{A}^{2}-O{K}^{2}}$=$\sqrt{5}$,
∵KH⊥OA,
∴KH=$\frac{OK•AK}{OA}$=2,OH=$\sqrt{O{K}^{2}-K{H}^{2}}$=4,
∴K(4,2),
∴直线OK的解析式为y=$\frac{1}{2}$x,
直线AD的解析式为y=-$\frac{1}{5}$x+1,
由$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=-\frac{1}{5}x+1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{10}{7}}\\{y=\frac{5}{7}}\end{array}\right.$,
∴OB与AD的交点P′($\frac{10}{7}$,$\frac{5}{7}$),
∴当点P与P′重合时,CP+DP最短时,点P的坐标为($\frac{10}{7}$,$\frac{5}{7}$),、
故选D.
点评 本题考查轴对称-最短问题、坐标与图形的性质、菱形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,学会构建一次函数解决交点问题,所以中考常考题型.

 如图,一条直线AB上有一点O,∠AOM=90°,∠COD=90°,∠COD在平角∠AOB内左右摆动(O点不动,OC与OA、OD与OB均不重合),在摆动时,除直角外,保持相等的角有( )
如图,一条直线AB上有一点O,∠AOM=90°,∠COD=90°,∠COD在平角∠AOB内左右摆动(O点不动,OC与OA、OD与OB均不重合),在摆动时,除直角外,保持相等的角有( )| A. | 一对 | B. | 两对 | C. | 三对 | D. | 四对 |
| A. |  | B. |  | C. |  | D. |  |
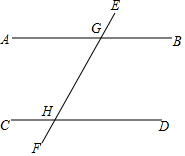 已知直线AB∥CD,EF交AB于G,交CD于H,若∠BGH的度数比∠GHD的2倍多10°,设∠BGH和∠GHD的度数分别为x、y,则下列正确的方程组为( )
已知直线AB∥CD,EF交AB于G,交CD于H,若∠BGH的度数比∠GHD的2倍多10°,设∠BGH和∠GHD的度数分别为x、y,则下列正确的方程组为( )| A. | $\left\{\begin{array}{l}{x+y=180°}\\{x=y+10°}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=180°}\\{x=2y+10°}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=180°}\\{x=2y-10°}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180°}\\{y=2x+10°}\end{array}\right.$ |
 (1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;
(1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;