题目内容
9.(1)计算:|$\sqrt{3}$-1|-($\frac{1}{2}$)-2-2sin60°(2)先化简,再求值:(1-$\frac{1}{a+1}$)-$\frac{{a}^{2}+2a+1}{a}$,其中a=$\sqrt{2}$-1.
分析 (1)根据谁说的运算法则,负指数幂的性质,特殊角的三角函数的值就是即可;
(2)根据分式的加减混合运算就是即可.
解答 解:(1)原式=$\sqrt{3}$-1-4-2×$\frac{\sqrt{3}}{2}$=-5;
(2)原式=$\frac{a+1-1}{a+1}$-$\frac{(a+1)^{2}}{a}$=a+1,
当a=2时,原式=$\sqrt{2}$+1-1=$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.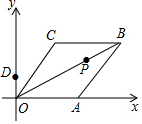 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )| A. | (1,$\frac{1}{2}$) | B. | ($\frac{4}{3}$,$\frac{2}{3}$) | C. | ($\frac{6}{5}$,$\frac{3}{5}$) | D. | ($\frac{10}{7}$,$\frac{5}{7}$) |
4.关于x的不等式x-m>0,恰有两个负整数解,则m的取值范围是( )
| A. | -3<m<-2 | B. | -3≤m<-2 | C. | -3≤m≤-2 | D. | -3<m≤-2 |
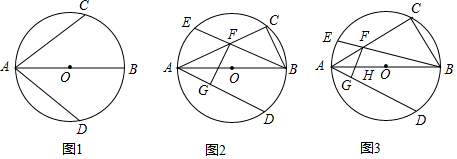
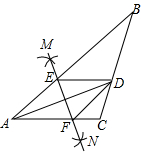 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:①分别以点A、D为圆心,以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于两点M、N;②连接MN分别交AB、AC于点E、F;③连接DE、DF.若BD=6,AF=4,CD=3,则下列说法中正确的是( )
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:①分别以点A、D为圆心,以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于两点M、N;②连接MN分别交AB、AC于点E、F;③连接DE、DF.若BD=6,AF=4,CD=3,则下列说法中正确的是( )