题目内容
15.如图,将一副三角尺的直角顶点重合在点O处.(1)若∠BOD=20°,分别求图1,图2中∠AOC的度数(0°<∠AOC<180°);
(2)直接写出∠AOC和∠BOD的大小关系;
(3)在图2中,当OD分∠AOB为2:3两部分,求∠AOC的度数.

分析 (1)根据周角的定义可得图1中∠AOC的度数,根据直角的定义和角的和差关系可得图2中∠AOC的度数;
(2)根据周角的定义可得图1中∠AOC和∠BOD的大小关系,根据直角的定义和角的和差关系可得图2中∠AOC和∠BOD的大小关系;
(3)分2种情况:①∠AOD:∠BOD=2:3;②∠BOD:∠AOD=2:3;进行讨论可求∠AOC的度数.
解答 解:(1)图1中∠AOC=360°-90°×2-20°=160°,
图2中∠AOC=90°×2-20°=160°;
(2)图1中∠AOC+∠BOD=180°,
图2中∠AOC+∠BOD=180°;
(3)①∠AOD:∠BOD=2:3,
∠AOD=90°×$\frac{2}{3+2}$=36°,
∠AOC=90°+36°=126°;
②∠BOD:∠AOD=2:3,
∠AOD=90°×$\frac{3}{3+2}$=54°,
∠AOC=90°+54°=144.
故∠AOC的度数是126°或144°.
点评 考查了余角和补角,是基础题,准确识别图形是解题的关键.

练习册系列答案
相关题目
5.若m>0,且m-$\frac{1}{m}$=3,则m+$\frac{1}{m}$等于( )
| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{13}$ | D. | $\sqrt{11}$ |
6.下列等式从左到右的变形,属于因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2+2x+1=x(x+2)+1 | C. | x2-2x=x(x-2) | D. | 4x2-6x=x(4x-6) |
3.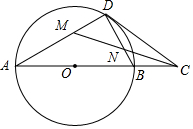 如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M
如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M
(1)求证:DM=DN
(2)若AB=6,BC=2,求tan∠ACM的值.
 如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M
如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M(1)求证:DM=DN
(2)若AB=6,BC=2,求tan∠ACM的值.
20.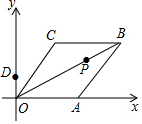 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )| A. | (1,$\frac{1}{2}$) | B. | ($\frac{4}{3}$,$\frac{2}{3}$) | C. | ($\frac{6}{5}$,$\frac{3}{5}$) | D. | ($\frac{10}{7}$,$\frac{5}{7}$) |
4.关于x的不等式x-m>0,恰有两个负整数解,则m的取值范围是( )
| A. | -3<m<-2 | B. | -3≤m<-2 | C. | -3≤m≤-2 | D. | -3<m≤-2 |
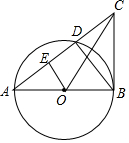 已知△ABC中,AB=8,BC=6,以AB为直径的⊙O与AC交于D点,连接BD,且BD=$\frac{24}{5}$.连接OC.
已知△ABC中,AB=8,BC=6,以AB为直径的⊙O与AC交于D点,连接BD,且BD=$\frac{24}{5}$.连接OC.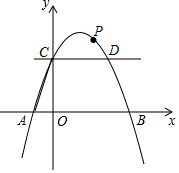 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,点A、B的坐标分别是(-1,0)、(5,0),与y轴交于点C,连接AC,过点C作CD∥x轴交抛物线于点D,点P是抛物线上一个动点,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,点A、B的坐标分别是(-1,0)、(5,0),与y轴交于点C,连接AC,过点C作CD∥x轴交抛物线于点D,点P是抛物线上一个动点,设点P的横坐标为m. 如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.
如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.