Question

14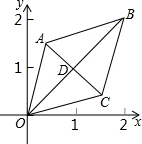．如图，已知菱形OABC的两个顶点O（0，0），B（2，2），若将菱形绕点O以每秒45°的速度逆时针旋转，则第2017秒时，菱形两对角线交点D的坐标为（0，$\sqrt{2}$）．

Answer 1

分析 根据菱形的性质及中点的坐标公式可得点D坐标，再根据旋转的性质可得旋转后点D的坐标．

解答 解：菱形OABC的顶点O（0，0），B（2，2），得
D点坐标为（$\frac{0+2}{2}$，$\frac{0+2}{2}$），即（1，1）．
每秒旋转45°，则第2017秒时，得45°×2017，
45°×2017÷360=252.125周，
OD旋转了252周半，菱形的对角线交点D的坐标为（0，$\sqrt{2}$），
故答案为：（0，$\sqrt{2}$）．

点评 本题主要考查菱形的性质及旋转的性质，熟练掌握菱形的性质及中点的坐标公式、中心对称的性质是解题的关键．