题目内容
7.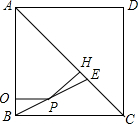
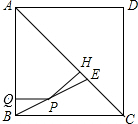 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 连接AP,过点E作EF⊥AB于点F,由正方形的性质可以得知AB=BC,∠BAC=45°,结合已知和三角函数值可求得EF的长度,由△ABE的面积=△ABP的面积+△AEP的面积,结合面积公式即可得出结论.
解答 解:连接AP,过点E作EF⊥AB于点F,如图所示.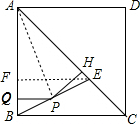
∵四边形ABCD为正方形,
∴AB=BC,∠BAC=∠DAC=45°.
∵AC=$\frac{BC}{sin∠BAC}$=2$\sqrt{2}$,
∴AB=BC=2.
∵AE=AB,
∴AE=2,EF=AE•sin∠FAE=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$.
△ABE的面积S△ABE=$\frac{1}{2}$AB•EF=S△ABP+S△AEP=$\frac{1}{2}$AB•PQ+$\frac{1}{2}$AE•PH=$\frac{1}{2}$AB×(PQ+PH),
∴PQ+PH=EF=$\sqrt{2}$.
故选B.
点评 本题考查了正方形的性质、三角形的面积公式以及特殊角的三角函数,解题的关键是:由△ABE的面积=△ABP的面积+△AEP的面积得出PQ+PH=EF.本题属于中档题,解题的技巧在于巧用面积公式.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 两角及一边分别相等的两个三角形全等 | |
| B. | 两边及一角分别相等的两个三角形全等 | |
| C. | 两腰分别相等的两个等腰三角形全等 | |
| D. | 底边及一腰分别相等的两个等腰三角形全等 |
16.学校体育节要组织一次班际乒乓球赛,参赛的每两个班之间都要比赛一场,根据场地和时间等条件,赛程计划安排15天,每天安排3场比赛.设有x个班参加比赛,则x满足的关系式为( )
| A. | x2=15×3 | B. | x(x-1)=15×3 | C. | $\frac{1}{2}x({x-1})=15×3$ | D. | $\frac{1}{2}x({x+1})=15×3$ |
 如图,?ABCD,AB=6,AD=9,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DF的长等于( )
如图,?ABCD,AB=6,AD=9,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DF的长等于( ) 探究问题.
探究问题. 在如图所示的方格纸上过点P画直线AB的平行线,过点P作PM⊥AB于点M.
在如图所示的方格纸上过点P画直线AB的平行线,过点P作PM⊥AB于点M.