题目内容
19.将抛物线y=-2x2-3向上平移若干个单位使抛物线与坐标轴有三个交点,如果这三个交点能构成直角三角形,那么平移的距离为$\frac{7}{2}$个单位.分析 设抛物线向上平移a(a>1)个单位,则有平移后抛物线的解析式为:y=-2x2-3+a,根据两个解析式得出A、M的坐标,得出OA的长,根据平移后的解析式得出B、C的坐标,得出BC的出,根据三角形斜边中线的性质得出a-3=$\sqrt{\frac{a-3}{2}}$,即可求得a的值.
解答  解:设抛物线向上平移a(a>1)个单位,使抛物线与坐标轴有三个交点,
解:设抛物线向上平移a(a>1)个单位,使抛物线与坐标轴有三个交点,
且这些交点能构成直角三角形,
则有平移后抛物线的解析式为:y=-2x2-3+a,AM=a,
∵抛物线y=-2x2-3与y轴的交点M为(0,-3),即OM=3,
∴OA=AM-OM=a-3,
令y=-2x2-3+a中y=0,得到-2x2-3+a=0,
解得:x=±$\sqrt{\frac{a-3}{2}}$,
∴B(-$\sqrt{\frac{a-3}{2}}$,0),C($\sqrt{\frac{a-3}{2}}$,0),即BC=2$\sqrt{\frac{a-3}{2}}$,
又△ABC为直角三角形,且B和C关于y轴对称,即O为BC的中点,
∴AO=$\frac{1}{2}$BC,即a-3=$\sqrt{\frac{a-3}{2}}$,
两边平方得:(a-3)2=$\frac{a-3}{2}$,
∵a-3≠0,∴a-3=$\frac{1}{2}$,
解得:a=$\frac{7}{2}$.
故答案为$\frac{7}{2}$.
点评 此题考查了二次函数的图象及几何变换,涉及的知识有:平移规律,直角三角形的性质,抛物线与x轴的交点,利用了转化及数形结合的思想,解题的关键是根据题意表示出OA及BC,利用直角三角形斜边上的中线等于斜边的一半建立两边长的关系,借助方程来解决问题.

练习册系列答案
相关题目
7.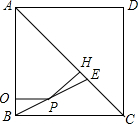
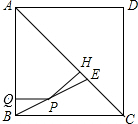 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )

 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
14.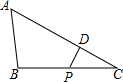 如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
 如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )| A. | 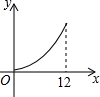 | B. | 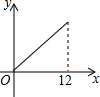 | C. | 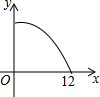 | D. | 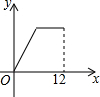 |
11.一个口袋中有红、白、黑球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一个球,记下颜色后放回袋中.不断重复这个过程,共摸了100次球,发现有49次摸到红球,21次摸到黑球,则袋中白球大约是( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
8.法国病毒学家团队2014年3月4日宣布,他们发现了世界上第三种超大型病毒,这种巨型史前病毒直径超过0.00000025米,0.0000005用科学记数法可表示为( )
| A. | 5×10-8 | B. | 5×10-9 | C. | 0.5×10-6 | D. | 0.05×10-5 |
 如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值.
如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值.