题目内容
14.若A=(2+1)(22+1)…(2n+1)+1,则A-2003的末位数字是( )| A. | 0 | B. | 3 | C. | 4 | D. | 6 |
分析 先添加因式(2-1),再连续运用平方差公式进行计算即可.
解答 解:因为A=(2+1)(22+1)…(2n+1)+1,
=(2-1)(2+1)(22+1)…(2n+1)+1,
=(22-1)(22+1)…(2n+1)+1,
=(24-1)(24+1)…(2n+1)+1,
=(28-1)(28+1)…(2n+1)+1,
…
=22n
=4n,
A的末位数字是4或6,
则A-2003的末位数字是1或3.
故选B.
点评 本题考查了平方差公式,关键在于添加因式(2-1)后构造成平方差公式结构,连续运用公式求解,另外掌握2的乘方的个位数的规律性循环也比较关键.

练习册系列答案
相关题目
5.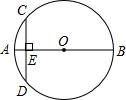 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{7}$ | C. | 6 | D. | 8 |
2.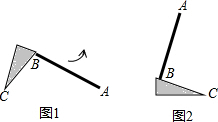 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )| A. | 75° | B. | 25° | C. | 115° | D. | 105° |
9.直线y=kx-1经过点A(-2,1),则不等式kx-1≥0的解集是( )
| A. | x≤-1 | B. | x≤0 | C. | x≥-1 | D. | x≥1 |
6.已知一列数:1,-2,3,-4,5,-6,7,…将这列数排成下列形式:
按照上述规律排下去,那么第100行从左边数第5个数是( )

按照上述规律排下去,那么第100行从左边数第5个数是( )
| A. | -4955 | B. | 4955 | C. | -4950 | D. | 4950 |
4.洛阳某中学“研究学习小组”的同学们进行了社会实践活动,其中一个小组的同学调查了30户家庭某月的用水量,如表所示:
则这30户家庭用水量的众数和中位数分别是( )
| 用水量(吨) | 15 | 20 | 25 | 30 | 41 |
| 户数 | 3 | 6 | 7 | 9 | 5 |
| A. | 25,27 | B. | 25,25 | C. | 30,27 | D. | 30,25 |
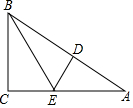 如图,在Rt△ABC中,∠ACB=90°,两条直角边CB、CA的长度分别为6,8,折叠△ABC,使点A、B重合,DE为折痕,连接BE,则cos∠BEC=$\frac{7}{25}$.
如图,在Rt△ABC中,∠ACB=90°,两条直角边CB、CA的长度分别为6,8,折叠△ABC,使点A、B重合,DE为折痕,连接BE,则cos∠BEC=$\frac{7}{25}$.