题目内容
2.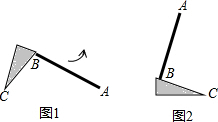 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )| A. | 75° | B. | 25° | C. | 115° | D. | 105° |
分析 连结AC并且延长至E,根据旋转的性质和平角的定义,由角的和差关系即可求解.
解答 解:如图:连结AC并且延长至E,
因为∠DCE=180°-∠DCB-∠ACB=105°,即旋转角为105°,
所以灰斗柄AB绕点C转动的角度为105°.
故选:D.
点评 本题考查了旋转的性质,解决本题的关键是由角的和差关系得到∠DCE的度数.解题时注意:对应点与旋转中心所连线段的夹角等于旋转角.

练习册系列答案
相关题目
13.一元二次方程(k-2)x2+kx+2=0(k≠2)的根的情况是( )
| A. | 该方程有两个不相等的实数根 | B. | 该方程有两个相等的实数根 | ||
| C. | 该方程有实数根 | D. | 该方程没有实数根 |
10.下列运算结果是a6的是( )
| A. | a2•a3 | B. | (-a2)3 | C. | (a2)3 | D. | a12-a6 |
7.下列运算正确的是( )
| A. | (-2ab)•(-3ab)3=-54a4b4 | B. | 5x2•(3x3)2=15x12 | ||
| C. | (-0.1b)•(-10b2)3=-b7 | D. | (3×10n)($\frac{1}{3}$×10n)=102n |
14.若A=(2+1)(22+1)…(2n+1)+1,则A-2003的末位数字是( )
| A. | 0 | B. | 3 | C. | 4 | D. | 6 |
11.$\sqrt{16}$的平方根是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 16 |
12.数轴上点A表示的数为$(\sqrt{5})^{2}$-13,则它的立方根是( )
| A. | -8 | B. | ±2 | C. | 2 | D. | -2 |
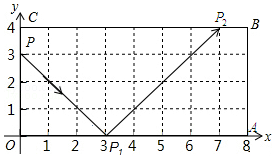 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4).
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4).