题目内容
 如图,四边形ABCD中,AD⊥DC,AC⊥CB,AC平分∠DAB,E为AB的中点.
如图,四边形ABCD中,AD⊥DC,AC⊥CB,AC平分∠DAB,E为AB的中点.(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求
| AC |
| AF |
考点:相似三角形的判定与性质
专题:
分析:(1)证明△ADC∽△ACB,得比例式AD:AC=AC:AB,即可得出结论;
(2)先证∠CAB=∠ACE,得出∠DAC=∠ACE,证出CE∥AD;
(3)由(1)先求出AC,再证明△AFD∽△CFE,得出比例式,AF:CF=AD:CE=4:3,即可证出结论.
(2)先证∠CAB=∠ACE,得出∠DAC=∠ACE,证出CE∥AD;
(3)由(1)先求出AC,再证明△AFD∽△CFE,得出比例式,AF:CF=AD:CE=4:3,即可证出结论.
解答:(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵AD⊥DC,AC⊥BC,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB•AD;
(2)证明:∵E为AB的中点,
∴CE=
AB=AE,
∴∠CAB=∠ACE,
∵∠DAC=∠CAB,
∴∠DAC=∠ACE,
∴CE∥AD;
(3)解:∵AC2=AB•AD=6×4=24,
∴AC=2
,
∵CE∥AD,
∴△AFD∽△CFE,
∴
=
,
∵CE=
AB=3,
∴
=
,
∴
=
,
∴
=
.
∴∠DAC=∠CAB,
∵AD⊥DC,AC⊥BC,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB•AD;
(2)证明:∵E为AB的中点,
∴CE=
| 1 |
| 2 |
∴∠CAB=∠ACE,
∵∠DAC=∠CAB,
∴∠DAC=∠ACE,
∴CE∥AD;
(3)解:∵AC2=AB•AD=6×4=24,
∴AC=2
| 6 |
∵CE∥AD,
∴△AFD∽△CFE,
∴
| AF |
| CF |
| AD |
| CE |
∵CE=
| 1 |
| 2 |
∴
| AF |
| CF |
| 4 |
| 3 |
∴
| AC |
| CF |
| 7 |
| 3 |
∴
| AC |
| AF |
| 7 |
| 4 |
点评:本题考查了相似三角形的判定与性质的综合运用,证明三角形相似得出比例式是解题的关键.

练习册系列答案
相关题目
 如图,已知AD是△ABC的高,把三角形纸片ABC折叠,使A点落在D处,折痕为EF,则下列结论中错误的是( )
如图,已知AD是△ABC的高,把三角形纸片ABC折叠,使A点落在D处,折痕为EF,则下列结论中错误的是( )| A、EF⊥AD | ||
B、EF=
| ||
C、DF=
| ||
D、DF=
|
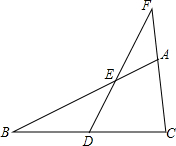 已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF.
已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF. 如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C(直线l不与线段AB相交),过A、B两点分别作直线l的垂线AE、BF,E、F为垂足.
如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C(直线l不与线段AB相交),过A、B两点分别作直线l的垂线AE、BF,E、F为垂足. 如图,在△ABC中,AB=AC,D是BC上一点,过点D作DE∥AB,且使DE=AC,连接AD,AE,EC.
如图,在△ABC中,AB=AC,D是BC上一点,过点D作DE∥AB,且使DE=AC,连接AD,AE,EC. 如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一条直线上,且AB=,BC=1,AG分别交DC,DE,FE于点P,Q,R.
如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一条直线上,且AB=,BC=1,AG分别交DC,DE,FE于点P,Q,R. 如图所示,是古城墙的一角,要测量墙角∠AOB的度数,但人又不能进入城墙,只能站在墙外,如何测量?请设计一种切实可行的测量方案,并说明你的理论根据.
如图所示,是古城墙的一角,要测量墙角∠AOB的度数,但人又不能进入城墙,只能站在墙外,如何测量?请设计一种切实可行的测量方案,并说明你的理论根据. 如图,∠1,∠2是直线
如图,∠1,∠2是直线