题目内容
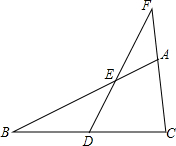 已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF.
已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF.考点:全等三角形的判定与性质,平行线的性质,等腰三角形的判定与性质
专题:证明题
分析:过点B作BG∥FC,延长FD交BG于点G.由平行线的性质可得∠G=∠F,然后判定△BDG和△CDF全等,根据全等三角形的性质和等量代换得到BE=BG,由等腰三角形的性质可得∠G=∠BEG,由对顶角相等及等量代换得出∠F=∠AEF,根据等腰三角形的判定得出AE=AF.
解答:证明:过点B作BG∥FC,延长FD交BG于点G.

∴∠G=∠F.
∵点D是BC的中点,
∴BD=CD.
在△BDG和△CDF中,
∴△BDG≌△CDF(AAS).
∴BG=CF.
∵BE=CF,
∴BE=BG.
∴∠G=∠BEG.
∵∠BEG=∠AEF,
∴∠G=∠AEF.
∴∠F=∠AEF.
∴AE=AF.

∴∠G=∠F.
∵点D是BC的中点,
∴BD=CD.
在△BDG和△CDF中,
|
∴△BDG≌△CDF(AAS).
∴BG=CF.
∵BE=CF,
∴BE=BG.
∴∠G=∠BEG.
∵∠BEG=∠AEF,
∴∠G=∠AEF.
∴∠F=∠AEF.
∴AE=AF.
点评:本题考查了全等三角形和等腰三角形的判定与性质,作出辅助线构造等腰三角形,并根据等腰三角形的性质得到三角形全等的条件是解题的基本思路.

练习册系列答案
相关题目
关于x的分式方程2k-4+
=
仅有一个实数根,则实数k的取值共有( )
| k+1 |
| x |
| k-5 |
| x+2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE. 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是 如图,四边形ABCD中,AD⊥DC,AC⊥CB,AC平分∠DAB,E为AB的中点.
如图,四边形ABCD中,AD⊥DC,AC⊥CB,AC平分∠DAB,E为AB的中点. 如图,⊙O1与⊙O2外切于A,PA是内公切线,BC是外公切线,B、C是切点.①△ABC是Rt△;②△PAB≌△O2AC;③BC2=4O1A•O2A;④以O1O2为直径的圆与BC恰好相切于点P.上述结论,正确结论的个数是( )
如图,⊙O1与⊙O2外切于A,PA是内公切线,BC是外公切线,B、C是切点.①△ABC是Rt△;②△PAB≌△O2AC;③BC2=4O1A•O2A;④以O1O2为直径的圆与BC恰好相切于点P.上述结论,正确结论的个数是( )