题目内容
9.已知m、n、k为非负实数,且m-k+1=2k+n=1,则代数式2k2-8k+6的最小值为$\frac{5}{2}$.分析 根据m、n是非负数列不等式组求出k的取值范围,再根据二次函数的增减性求解即可.
解答 解:∵m-k+1=2k+n=1,
∴m=k,n=1-2k,
∵m、n、k为非负实数,
∴$\left\{\begin{array}{l}{k≥0}\\{1-2k≥0}\end{array}\right.$,
解得0≤k≤$\frac{1}{2}$,
令y=2k2-8k+6=2(k-2)2-2,
∴当k=$\frac{1}{2}$,y有最小值2×($\frac{1}{2}$-2)2-2=$\frac{5}{2}$.
即代数式2k2-8k+6的最小值为$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了二次函数的最值问题,非负数的性质,难点在于列出不等式组然后求出k的取值范围,要注意利用二次函数的增减性求最值的方法.

练习册系列答案
相关题目
18.有下面几个样本用以统计某路口在学校放学时段的车流量情况.其中你认为合适的是( )
| A. | 抽取两天作为一个样本 | |
| B. | 选取每周星期日为样本 | |
| C. | 春、夏、秋、冬每个季节各选两周作为样本 | |
| D. | 以全年每一天为样本 |
19. 如图,∠1=30°,则射线OA表示为( )
如图,∠1=30°,则射线OA表示为( )
 如图,∠1=30°,则射线OA表示为( )
如图,∠1=30°,则射线OA表示为( )| A. | 南偏西60° | B. | 南偏西30° | C. | 南偏东60° | D. | 南偏东30° |
 如图所示,已知OB⊥OA,直线CD过点O,且∠AOC=35°,则∠BOD=125°.
如图所示,已知OB⊥OA,直线CD过点O,且∠AOC=35°,则∠BOD=125°.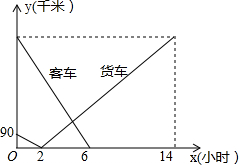 在一平直公路上依次有A、C、B三地,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车2小时可到达途中C站,14小时到达A地,客车需6小时到达C站.已知客车、货车到C站的距离与它们行驶时间x(小时)之间的函数关系如图所示,客车的速度比货车的速度快45千米/小时.
在一平直公路上依次有A、C、B三地,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车2小时可到达途中C站,14小时到达A地,客车需6小时到达C站.已知客车、货车到C站的距离与它们行驶时间x(小时)之间的函数关系如图所示,客车的速度比货车的速度快45千米/小时.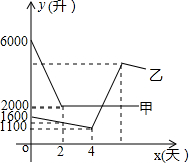 随着哈尔滨汽车的增加,哈市某乙储油库的储油量一直以每天相同的速度持续减少.为保证用户用油量,大庆某甲储油库立即以管道运输方式向哈市的乙储油库输油2天.如图,是两储油库的储油量y(升)与时间x(天)之间的函数图象.在单位时间内,甲储油库的放油量与乙储油库的进油量相同(油在排放、接收以及输送过程中的损耗不计).下列四种说法:
随着哈尔滨汽车的增加,哈市某乙储油库的储油量一直以每天相同的速度持续减少.为保证用户用油量,大庆某甲储油库立即以管道运输方式向哈市的乙储油库输油2天.如图,是两储油库的储油量y(升)与时间x(天)之间的函数图象.在单位时间内,甲储油库的放油量与乙储油库的进油量相同(油在排放、接收以及输送过程中的损耗不计).下列四种说法: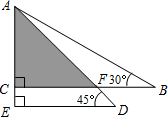 将一副三角尺按如图所示叠放在一起,若AB=12cm,则阴影部分的面积是18cm2.
将一副三角尺按如图所示叠放在一起,若AB=12cm,则阴影部分的面积是18cm2.