题目内容
1.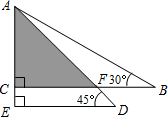 将一副三角尺按如图所示叠放在一起,若AB=12cm,则阴影部分的面积是18cm2.
将一副三角尺按如图所示叠放在一起,若AB=12cm,则阴影部分的面积是18cm2.
分析 由于BC∥DE,那么△ACF也是等腰直角三角形,欲求其面积,必须先求出直角边AC的长;Rt△ABC中,已知斜边AB及∠B的度数,易求得AC的长,进而可根据三角形面积的计算方法求出阴影部分的面积.
解答 解:∵∠B=30°,∠ACB=90°,AB=16cm,
∴AC=8cm.
由题意可知BC∥ED,
∴∠AFC=∠ADE=45°,
∴AC=CF=6cm.
故S△ACF=$\frac{1}{2}$×6×6=18(cm2).
故答案为:18.
点评 本题考查了相似三角形的判定和性质以及解直角三角形,发现△ACF是等腰直角三角形,并能根据直角三角形的性质求出直角边AC的长,是解答此题的关键.

练习册系列答案
相关题目
12. 如图,点p是x轴上的一个动点,过点p作x轴的垂线,交双曲线$y=\frac{k}{x}(k≠0)$于点Q,连接OQ,当点p沿x轴的正半轴方向运动时,Rt△POQ的面积( )
如图,点p是x轴上的一个动点,过点p作x轴的垂线,交双曲线$y=\frac{k}{x}(k≠0)$于点Q,连接OQ,当点p沿x轴的正半轴方向运动时,Rt△POQ的面积( )
 如图,点p是x轴上的一个动点,过点p作x轴的垂线,交双曲线$y=\frac{k}{x}(k≠0)$于点Q,连接OQ,当点p沿x轴的正半轴方向运动时,Rt△POQ的面积( )
如图,点p是x轴上的一个动点,过点p作x轴的垂线,交双曲线$y=\frac{k}{x}(k≠0)$于点Q,连接OQ,当点p沿x轴的正半轴方向运动时,Rt△POQ的面积( )| A. | 逐渐增大 | B. | 不变 | C. | 逐渐减小 | D. | 无法确定 |
16.通过平移y=-2(x-1)2+3的图象,可得到y=-2x2的图象,下列平移方法正确的是( )
| A. | 向左移动1个单位,向上移动3个单位 | |
| B. | 向右移动1个单位,向上移动3个单位 | |
| C. | 向左移动1个单位,向下移动3个单位 | |
| D. | 向右移动1个单位,向下移动3个单位 |
10.甲箱装有40个红球和10个黑球,乙箱装有60个红球、40个黑球和50个白球.这些球除了颜色外没有其他区别.搅匀两箱中的球,从箱中分别任意摸出一个球.从甲、乙两箱中摸到黑球的概率分别用P甲、P乙表示,则( )
| A. | P甲>P乙 | B. | P甲<P乙 | ||
| C. | P甲=P乙 | D. | 无法比较P甲、P乙的大小 |
11.实数$\sqrt{3}-2$的绝对值是( )
| A. | $\sqrt{3}-2$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}+2$ | D. | 1 |
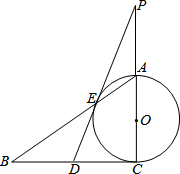 如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点E,D是BC的中点,DE的延长线交CA的延长线于点P.
如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点E,D是BC的中点,DE的延长线交CA的延长线于点P.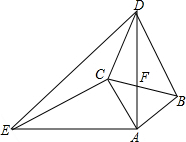 如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.