题目内容
17.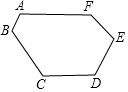 如图所示,六边形ABCDEF的六个内角都相等,若AB=1,BC=CD=3,DE=2,求这个六边形的周长.
如图所示,六边形ABCDEF的六个内角都相等,若AB=1,BC=CD=3,DE=2,求这个六边形的周长.
分析 由于已知四条边的长度,所以问题实质上是求AF和EF,由于六边形每个内角相等,即每个角都是120度,分别过点B、D、F作三组对边的平行线,可得出三个平行四边形,同时三条线在六边形中间交出一个等边三角形,从而利用平行四边形和等边三角形的性质即可求出AF和EF.
解答 解:如图,作BK∥AF,DG∥EF,FH∥DE,
BK交DG于G,FH交BK于K,FH交DG于H,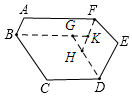
∵六边形ABCDEF的六个内角都相等,
∴∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=∠FAB=120°,
∵AF∥BK,
∴∠ABK=180°-∠BAF=60°,
∴∠CBK=60°,
∴BK∥CD,
同理DG∥BC,FH∥AB,
∴ABKF、BCDG、HDEF均为平行四边形,
∴BG=DG=CD=BC=3,FH=DE=2,FK=AB=1,
∵∠CBK=60°,BCDG是平行四边形,
∴∠KGH=60°,
同理∠GHK=60°,
∴△GHK是等边三角形,
∴GK=GH=HK=FH-FK=DE-AB=1,
∴AF=BK=BG+GK=CD+GK=3+1=4,
EF=HD=DG-GH=3-1=2,
∴六边形ABCDEF的周长为AB+BC+CD+DE+EF+FA=1+3+3+2+2+4=15.
点评 本题主要考查了多边形的内角和性质、平行四边形的判定与性质、等边三角形的判定与性质,题目小而巧,是一道锻炼学生空间构思能力的好题.作出平行线构造出平行四边形和等边三角形是解答本题的关键所在.

练习册系列答案
相关题目
7.蜗牛从树根沿着树干往上爬,白天爬上4米,夜间滑下3米,那么高7米的树,蜗牛爬到树顶要( )
| A. | 3天 | B. | 4天 | C. | 5天 | D. | 6天 |
5.滕州市某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
经统计发现两班总数相等,此时有学生建议,可以通过考察数据中的其他信息作为参考,请你回答下列问题:
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
12.某学校计划选一名跳高运动员参加一项校际比赛,对甲、乙两名跳高运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
教练组对这些数据进行了分析处理,求得:甲运动员的平均成绩为168cm,方差为31.5;乙运动员的平均成绩为169cm.
(1)求乙运动员这8次比赛成绩的方差;
(2)这两人中谁的成绩更稳定?说明理由;
(3)据预测,在校际比赛中需跳过170cm才可能获得冠军,该校为了获得跳高比赛冠军,可能选择哪位运动员参赛?
| 甲 | 160 | 173 | 172 | 161 | 162 | 171 | 170 | 175 |
| 乙 | 170 | 165 | 168 | 169 | 172 | 173 | 168 | 167 |
(1)求乙运动员这8次比赛成绩的方差;
(2)这两人中谁的成绩更稳定?说明理由;
(3)据预测,在校际比赛中需跳过170cm才可能获得冠军,该校为了获得跳高比赛冠军,可能选择哪位运动员参赛?
9.某中学生军训,沿着与笔直的铁路并列的公路匀速前进,每小时走4500米,一列火车以每小时120千米的速度迎面开来,测得火车与队首学生相遇,到车尾与队末学生相遇共经过60秒,如果队伍长500米,那么火车长( )
| A. | 1500米 | B. | 1575米 | C. | 2000米 | D. | 2075米 |
 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.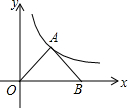 已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.
已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.