题目内容
19．网络时代的到来，很多家庭都接入了网络，电信局规定了拨号入网两种收费方式，用户可以任选其一；①某用户某月上网的时间为x小时，两种收费方式的费用分别为yA（元）、yB（元）．写出yA、yB与x之间的函数关系式；
②在上网时间相同的条件下，请你帮该用户选择哪种方式上网更省钱？
| 月租费（元） | 计费方式（元/分） | |
| A方式 | 0 | 0.05 |
| B方式 | 54 | 0.02 |
分析 （1）0.05元/分=3元/时，0.02元/分=1.2元/时，y1=每小时收费额×小时数，y2=每小时收费额×小时数+月租费；
（2）分别求出y1＜y2，y1=y2，y1＞y2时x的取值范围，根据x的取值范围选择入网的方式．
解答 解：（1）y1=3x（x＞0），y2=1.2x+54（x＞0）；
（2）由y1＜y2得，3x＜1.2x+54，解得x＜30；
由y1=y2得，3x=1.2x+54，解得x=30；
由y1＞y2得，3x＞1.2x+54，解得x＞30；
综上所述：当该用户上网时间少于30小时时，选择计时制上网省钱；
当上网时间等于30小时时选择计时制、全月制费用一样；
当上网时间超过30小时时选择全月制上网省钱．
点评 此题考查一次函数的应用，求出费用相同的通话时间，因为比例系数为3与1.2可知长于该时间省钱方案．
练习册系列答案
相关题目
9．下列各式属于最简二次根式的是（ ）
| A． | $\sqrt{18}$ | B． | -$\frac{1}{2}\sqrt{3}$ | C． | $\frac{1}{\sqrt{2}}$ | D． | $\sqrt{\frac{1}{5}}$ |
如图，函数y=2x和y=ax+4的图象和交于点A（m，3），则不等式2x≥ax+4的解集为x≥1.5．
14．已知一次函数y=（1+2m）x-1中，函数值y随自变量x的增大而减小，那么m取值范围是（ ）
| A． | m＜-$\frac{1}{2}$ | B． | m≥-$\frac{1}{2}$ | C． | m≤-$\frac{1}{2}$ | D． | m＞-$\frac{1}{2}$ |
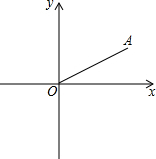如图，在平面直角坐标系中，点A坐标为（2，1），连接OA，点P是x轴上的一动点，如果△OAP是等腰三角形，请你写出符合条件的点P坐标P1（4，0），P2（$\sqrt{5}$，0），P3（-$\sqrt{5}$，0），P4（$\frac{5}{4}$，0）．
11．若点P（3，2-m）在函数y=$\frac{1}{x}$的图象上，则点P一定在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |