题目内容
14.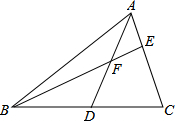 如图,在△ABC中,AD为BC边上的中线,E为AC上的一点,BE交AD于点F,已知AE=EF.求证:AC=BF.
如图,在△ABC中,AD为BC边上的中线,E为AC上的一点,BE交AD于点F,已知AE=EF.求证:AC=BF.
分析 延长AD到G,使得DG=AD,先证明△ADC≌△GDB,得AC=BG,证明BG=BF即可解决问题.
解答 证明:延长AD到G,使得DG=AD.
在△ADC和△GDB中,
$\left\{\begin{array}{l}AD=GD\\∠ADC=∠GDB\\ CD=BD\end{array}\right.$,
∴△ADC≌△GDB,
∴AC=BG 且∠CAD=∠G
∵AE=EF,
∴∠EFA=∠EAF,
∴∠G=∠EFA,
∵∠EFA=∠BFG,
∴∠G=∠BFG,
∴BG=BF,
∵AC=BG,
∴BF=AC.
点评 本题考查全等三角形的判定和性质,三角形中线的性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
5.如果关于x的方程ax2-3x+2=0是一元二次方程,那么a取值范围是( )
| A. | a>0 | B. | a≥0 | C. | a=1 | D. | a≠0 |
6. 如图,在?ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )
如图,在?ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )
 如图,在?ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )
如图,在?ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
16.若一次函数y=kx-b的图象经过第二、三、四象限,则k,b的取值范围是( )
| A. | k>0,b>0 | B. | k<0,b>0 | C. | k<0,b<0 | D. | k<0,b>0 |
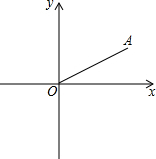 如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标P1(4,0),P2($\sqrt{5}$,0),P3(-$\sqrt{5}$,0),P4($\frac{5}{4}$,0).
如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标P1(4,0),P2($\sqrt{5}$,0),P3(-$\sqrt{5}$,0),P4($\frac{5}{4}$,0). 如图,在Rt△ABC中,∠C=90°,AC=6,AB=10,DE垂直平分AB,分别交AB、BC于点D、E.求CE的长.
如图,在Rt△ABC中,∠C=90°,AC=6,AB=10,DE垂直平分AB,分别交AB、BC于点D、E.求CE的长.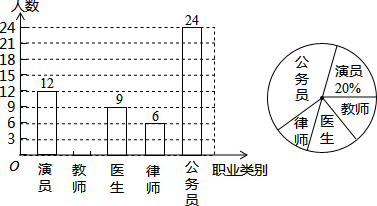
 如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=5(提示:可连接BE)
如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=5(提示:可连接BE)