题目内容
 如图,⊙O的两条直径AB、CD互相垂直,弦MN垂直平分OB,交OB于点E,求证:MB与MC分别为该圆的内接正六边形和正十二边形的边长.
如图,⊙O的两条直径AB、CD互相垂直,弦MN垂直平分OB,交OB于点E,求证:MB与MC分别为该圆的内接正六边形和正十二边形的边长.考点:正多边形和圆
专题:证明题
分析:如图,作辅助线,求出∠MOB、∠MOC的度数,即可解决问题.
解答: 解:如图,连接OM;
解:如图,连接OM;
∵弦MN垂直平分OB,
∴MB=MO,OE=
OM,
∴∠OME=30°;而BO=MO,
∴△MOB是等边三角形,∠MOB=60°;
∵⊙O内接正六边形的中心角=
×360°=60°,
∴MB为⊙O内接正六边形的边;
∵MN⊥AB,CD⊥AB,
∴MN∥CD,∠COM=∠OME=30°,
∵⊙O内接正十二边形的中心角=
×360°=30°,
∴CM为⊙O内接正十二边形的边.
 解:如图,连接OM;
解:如图,连接OM;∵弦MN垂直平分OB,
∴MB=MO,OE=
| 1 |
| 2 |
∴∠OME=30°;而BO=MO,
∴△MOB是等边三角形,∠MOB=60°;
∵⊙O内接正六边形的中心角=
| 1 |
| 6 |
∴MB为⊙O内接正六边形的边;
∵MN⊥AB,CD⊥AB,
∴MN∥CD,∠COM=∠OME=30°,
∵⊙O内接正十二边形的中心角=
| 1 |
| 12 |
∴CM为⊙O内接正十二边形的边.
点评:该题主要考查了正多边形和圆的关系及其应用问题;解题的关键是深入分析、大胆猜想、合情推理、科学论证.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
用四舍五入法按要求对501923分别取近似值,其中正确的是( )
| A、5.0×105(精确到十万位) |
| B、5.01×105(精确到百分位) |
| C、5.02×105(精确到千位) |
| D、5.019×105(精确到0.01) |
在-2,+3.5,0,-
,-0.7,11中,负分数有( )
| 2 |
| 3 |
| A、l个 | B、2个 | C、3个 | D、4个 |
把ad=bc写成比例式,写错的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
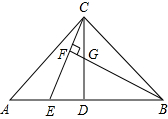 已知:在△ABC中,AC=BC,∠ACB=90°,CD⊥AB,点E是AB边上一点.直线BF⊥CE于点F,交CD于点G(如图),求证:
已知:在△ABC中,AC=BC,∠ACB=90°,CD⊥AB,点E是AB边上一点.直线BF⊥CE于点F,交CD于点G(如图),求证: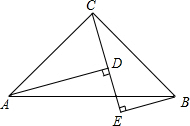 如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2cm,则BE的长为
如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2cm,则BE的长为