题目内容
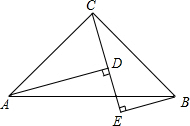 如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2cm,则BE的长为
如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2cm,则BE的长为考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:根据题中给出的条件易证△ACD≌△CBE,根据全等三角形对应边相等的性质可得AD=CE,CD=BE,即可求得CD的长,即可解题.
解答:解:∵∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴BE=CD=CE-DE=AD-DE=3cm,
故答案为 3.
∴∠CAD=∠BCE,
在△ACD和△CBE中,
|
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴BE=CD=CE-DE=AD-DE=3cm,
故答案为 3.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△CBE是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 (2)已知乙车以60km/时的速度匀速行驶,设行驶过程中,两车的距离为s(km),请直接写出s关于x的表达式;
(2)已知乙车以60km/时的速度匀速行驶,设行驶过程中,两车的距离为s(km),请直接写出s关于x的表达式; 如图,AB为⊙O的直径,且AB⊥CD于点E,CD=16,AE=4,求DE的长.
如图,AB为⊙O的直径,且AB⊥CD于点E,CD=16,AE=4,求DE的长. 如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E,求证:DE=BD+CE.
如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E,求证:DE=BD+CE. 如图,⊙O的两条直径AB、CD互相垂直,弦MN垂直平分OB,交OB于点E,求证:MB与MC分别为该圆的内接正六边形和正十二边形的边长.
如图,⊙O的两条直径AB、CD互相垂直,弦MN垂直平分OB,交OB于点E,求证:MB与MC分别为该圆的内接正六边形和正十二边形的边长.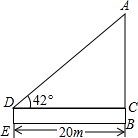 如图,升国旗时,某同学站在离国旗20m处行注目礼,当国旗升至顶端时,该同学视线的仰角为42°,已知双眼离地面1.60m,求旗杆AB的高度(精确到0.01m).
如图,升国旗时,某同学站在离国旗20m处行注目礼,当国旗升至顶端时,该同学视线的仰角为42°,已知双眼离地面1.60m,求旗杆AB的高度(精确到0.01m). 如图,BD是∠ABC的平分线,DE⊥AB,垂足为E,S△ABC=36cm2,AB=18cm,BC=6cm,则DE=
如图,BD是∠ABC的平分线,DE⊥AB,垂足为E,S△ABC=36cm2,AB=18cm,BC=6cm,则DE=