题目内容
6. 如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为$\frac{π}{2}$.
如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为$\frac{π}{2}$.
分析 根据30°角所对的直角边等于斜边的一半求出AB的长度,再根据勾股定理求出AC的长度,然后根据中点定义求出DB、CE的长度,再利用勾股定理求出BE的长度,然后根据旋转变换的性质可得阴影部分的面积等于以BE为半径的扇形面积减去以DB为半径的扇形的面积,然后列式进行计算即可得解.
解答 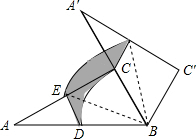 解:∵∠ACB=90°,∠A=30°,BC=2,
解:∵∠ACB=90°,∠A=30°,BC=2,
∴AB=2BC=4,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵D、E分别为AB、AC的中点,
∴DB=$\frac{1}{2}$AB=2,CE=$\frac{1}{2}$AC=$\sqrt{3}$,
在Rt△BCE中,BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$,
∵旋转角度为120°,
∴阴影部分的面积=$\frac{60•π•B{E}^{2}}{360}$-$\frac{60•π•B{D}^{2}}{360}$=$\frac{7π-4π}{6}$=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查了扇形的面积计算,直角三角形的性质,旋转变换的性质,观察出阴影部分的面积的表示是解题的关键.

练习册系列答案
相关题目
8.下列说法错误的是( )
| A. | 一个角的补角比它的余角大 | B. | 若两角相等,则它们的补角也相等 | ||
| C. | 相等的角是对顶角 | D. | 两个钝角不能互补 |
 如图,已知AB∥CD,∠ECD=∠EDC,求证:∠AEC=∠BED.
如图,已知AB∥CD,∠ECD=∠EDC,求证:∠AEC=∠BED.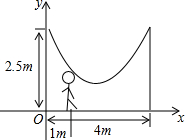 如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子.
如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子.
 数轴上有理数a,b,c所对应的点位置如图,且b与c所对应的点到原点O的距离相等,请先判断|a+b|,|b+c|和|c-a|,再化简|a+b|+|b+c|-|c-a|.
数轴上有理数a,b,c所对应的点位置如图,且b与c所对应的点到原点O的距离相等,请先判断|a+b|,|b+c|和|c-a|,再化简|a+b|+|b+c|-|c-a|.