题目内容
4.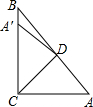 如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )
如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
分析 根据折叠性质得出∠DCA=∠BCD=45°,∠CDA=∠CDA′,求出∠CDA、∠CDA′,根据三角形外角性质求出∠BDC,即可求出答案.
解答 解:∵将△ACD折叠,使点A落在边CB上A′处,折痕为CD,∠ACB=90°,
∴∠DCA=∠BCD=45°,∠CDA=∠CDA′,
∴∠CDA=180°-∠DCA-∠A=180°-45°-50°=85°,
∴∠CDA′=85°,
∵∠BDC=∠A+∠DCA=50°+45°=95°,
∴∠A′DB=∠BDC-∠A′DC=95°-85°=10°.
故选:D.
点评 本题考查了折叠性质,三角形外角性质,三角形内角和定理的应用,关键是求出∠BDC和∠A′DC的度数.

练习册系列答案
相关题目
9. 如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )
如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )
 如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )
如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )| A. | 1:2 | B. | 2:5 | C. | 3:5 | D. | 1:3 |
16.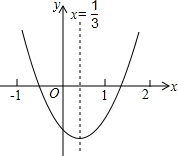 小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
①c<0;②abc<0;③a-b+c>0;④2a-3b=0;⑤4a+2b+c>0.
你认为其中正确的是( )
 小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0;②abc<0;③a-b+c>0;④2a-3b=0;⑤4a+2b+c>0.
你认为其中正确的是( )
| A. | ①②④ | B. | ①③⑤ | C. | ②③⑤ | D. | ①③④⑤ |
13.一元二次方程x2=4的根为( )
| A. | x=2 | B. | x=-2 | C. | x1=2,x2=-2 | D. | x=4 |
14.如果α是锐角,且cosα=$\frac{4}{5}$,那么sinα的值( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |