题目内容
 已知,如图,在△ABC中,内切圆I与边BC,CA,AB分别相交于点D,E,F.求证:∠FDE=90°-
已知,如图,在△ABC中,内切圆I与边BC,CA,AB分别相交于点D,E,F.求证:∠FDE=90°-| 1 |
| 2 |
考点:三角形的内切圆与内心
专题:证明题
分析:连结IE、IF,如图,根据切线的性质得到∠AEI=∠AFI=90°,则利用四边形内角和得到∠A+∠EIF=180°,再由圆周角定理得∠EIF=2∠FDE,所以∠A+2∠EDF=180°,然后变形即可得到结论.
解答:证明:连结IE、IF,如图,
∵内切圆I与边CA,AB分别相交于点E,F,
∴IE⊥AC,IF⊥AB,
∴∠AEI=∠AFI=90°,
∴∠A+∠EIF=180°,
∵∠EIF=2∠FDE,
∴∠A+2∠EDF=180°,
∴∠FDE=90°-
∠A.

∵内切圆I与边CA,AB分别相交于点E,F,
∴IE⊥AC,IF⊥AB,
∴∠AEI=∠AFI=90°,
∴∠A+∠EIF=180°,
∵∠EIF=2∠FDE,
∴∠A+2∠EDF=180°,
∴∠FDE=90°-
| 1 |
| 2 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.熟练运用切线的性质.

练习册系列答案
相关题目
下列各数与2的和是0的是( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 如图,直线l1∥l2,AB⊥CD,∠1=30°,∠2的度数=
如图,直线l1∥l2,AB⊥CD,∠1=30°,∠2的度数= 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF,其中正确的序号是
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF,其中正确的序号是 如图,将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,已知AC=8cm,BC=6cm,求线段DD′的长.
如图,将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,已知AC=8cm,BC=6cm,求线段DD′的长. 如图,在Rt△ABC中∠ABC=90°,BA=BC,P在△ABC的内部,且∠APB=135°,PA:PC=1:3,求PA:PB.
如图,在Rt△ABC中∠ABC=90°,BA=BC,P在△ABC的内部,且∠APB=135°,PA:PC=1:3,求PA:PB.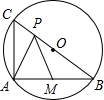 如图,BC为⊙O的直径,BC=2
如图,BC为⊙O的直径,BC=2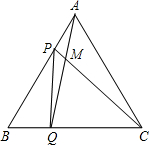 如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒
如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒 如图,AB是⊙O的切线,切点为C,则图中成立的结论有
如图,AB是⊙O的切线,切点为C,则图中成立的结论有