题目内容
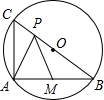 如图,BC为⊙O的直径,BC=2
如图,BC为⊙O的直径,BC=2| 2 |
考点:轴对称-最短路线问题,圆心角、弧、弦的关系
专题:
分析:连接CM则m的最大值为P移动到B、C点时△ACM的周长,根据勾股定理即可求得CM的长,进而求得△ACM的周长;作AA′⊥BC,交⊙O于A′,连接A′B、A′C,则四边形ABA′C是正方形,作MM′⊥BC交A′B于M′,则M′与M关于BC对称,连接AM′交BC于P′,P′A+P′M=AM′,此时△PAM的周长为m最小;
根据勾股定理求得AM′的长,进而求得△AP′M的周长,即可求得m的取值范围.
根据勾股定理求得AM′的长,进而求得△AP′M的周长,即可求得m的取值范围.
解答: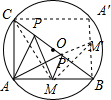 解:∵⊙O的直径BC=2
解:∵⊙O的直径BC=2
,
∴∠CAB=90°,
∵
=
,
∴∠B=∠C=45°,
∴AC=AB=2,
∴AM=
AB=1,
连接CM,则CM=
=
,
∴m的最大值为2+1+
=3+
,
作AA′⊥BC,交⊙O于A′,连接A′B、A′C,则四边形ABA′C是正方形,
作MM′⊥BC交A′B于M′,则M′与M关于BC对称,连接AM′交BC于P′,P′A+P′M=AM′,此时△PAM的周长为m最小;
∵A′B=AB=2,M为AB的中点,
∴BM′=BM=1,
∵AM′=
,
∴m的最小值为1+
,
∴m的取值范围是1+
≤m≤3+
.
故答案为1+
≤m≤3+
.
 解:∵⊙O的直径BC=2
解:∵⊙O的直径BC=2| 2 |
∴∠CAB=90°,
∵
 |
| AB |
 |
| AC |
∴∠B=∠C=45°,
∴AC=AB=2,
∴AM=
| 1 |
| 2 |
连接CM,则CM=
| AC2+AM2 |
| 5 |
∴m的最大值为2+1+
| 5 |
| 5 |
作AA′⊥BC,交⊙O于A′,连接A′B、A′C,则四边形ABA′C是正方形,
作MM′⊥BC交A′B于M′,则M′与M关于BC对称,连接AM′交BC于P′,P′A+P′M=AM′,此时△PAM的周长为m最小;
∵A′B=AB=2,M为AB的中点,
∴BM′=BM=1,
∵AM′=
| 5 |
∴m的最小值为1+
| 5 |
∴m的取值范围是1+
| 5 |
| 5 |
故答案为1+
| 5 |
| 5 |
点评:本题考查了轴对称-最短路线问题以及轴对称的性质,勾股定理的应用,正方形的判定及性质,解决本题的关键是确定AP+PM的最大值和最小值.

练习册系列答案
相关题目
下列命题中是假命题的是( )
| A、平行四边形的对边相等 |
| B、菱形的四条边相等 |
| C、矩形的对边平行且相等 |
| D、平行四边形的对角线相等 |
 已知,如图,在△ABC中,内切圆I与边BC,CA,AB分别相交于点D,E,F.求证:∠FDE=90°-
已知,如图,在△ABC中,内切圆I与边BC,CA,AB分别相交于点D,E,F.求证:∠FDE=90°- 如图,在△OAB中,∠AOB=25°,将△OAB绕点顶O顺时针旋转60°得到△COD,观察图形并回答问题:
如图,在△OAB中,∠AOB=25°,将△OAB绕点顶O顺时针旋转60°得到△COD,观察图形并回答问题: 如图,AB=AC,点D、E分别在线段AB、AC上,连接BE、CD交于点0,∠B=∠C,求证:OB=OC.
如图,AB=AC,点D、E分别在线段AB、AC上,连接BE、CD交于点0,∠B=∠C,求证:OB=OC.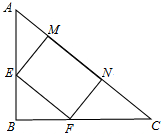 如图,在Rt△ABC中,AC=40,BC=30,在其内部挖出一个矩形,问挖出的矩形的最大面积是多少?
如图,在Rt△ABC中,AC=40,BC=30,在其内部挖出一个矩形,问挖出的矩形的最大面积是多少?