题目内容
12.对于y=k2x(k≠0)的图象下列说法不正确的是( )| A. | 是一条直线 | B. | 过点($\frac{1}{k}$,k) | ||
| C. | 经过一、三象限或二、四象限 | D. | y随x增大而增大 |
分析 根据y=k2x(k≠0),可知k2>0,从而可知y=k2x(k≠0)的图象的情况,从而可以解答本题.
解答 解:∵y=k2x(k≠0),
∴k2>0.
∴y=k2x(k≠0)的图象是正比例函数的图象,图象在第一、三象限,y随x的增大而增大,图象是一条直线.
当x=$\frac{1}{k}$时,y=k2x=${k}^{2}×\frac{1}{k}=k$.
即y=k2x(k≠0)的图象过点($\frac{1}{k},k$).
由上可得,选项A的说法正确,选项B的说法正确,选项C的说法不正确,选项D的说法正确.
故选C.
点评 本题考查的是正比例函数的性质,解题的关键是明确在正比例函数y=kx(k≠0)中:当k>0时,函数图象过一、三象限,y随x的增大而增大;当k<0时,函数图象过二、四象限,y随x的增大而减小.

练习册系列答案
相关题目
5.若a为方程x2-x-5=0的解,则a-a2+1的值是( )
| A. | -6 | B. | 6 | C. | -4 | D. | 4 |
17. 如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )
如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )
 如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )
如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )| A. | 40° | B. | 50° | C. | 80° | D. | 100° |
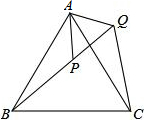 如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.
如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.