题目内容
某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,为了保证花苗的质量,每盆花苗的株数不超过6株,要使每盆的盈利达到20元,每盆应该植多少株?
考点:一元二次方程的应用
专题:
分析:根据已知假设每盆花苗增加x株,则每盆花苗有(x+3)株,得出平均单株盈利为(5-0.5x)元,由题意得(x+3)(5-0.5x)=20求出即可.
解答:解:设每盆应该多植x株,由题意得
(3+x)(5-0.5x)=20,
解得:x1=2,x2=5.
因为要且尽可能地减少成本,所以x2=5舍去,
2+3=5.
答:每盆植5株时,每盆的盈利20元.
(3+x)(5-0.5x)=20,
解得:x1=2,x2=5.
因为要且尽可能地减少成本,所以x2=5舍去,
2+3=5.
答:每盆植5株时,每盆的盈利20元.
点评:此题考查了一元二次方程的应用,根据每盆花苗株数×平均单株盈利=总盈利得出方程是解题关键.

练习册系列答案
相关题目
方程x2-6x+1=0经过配方后,其结果正确的是( )
| A、(x-3)2=8 |
| B、(x+3)2=35 |
| C、(x-3)2=35 |
| D、(x+3)2=8 |
下列几组数中互为相反数的是( )
A、-
| ||
B、
| ||
| C、-(-6)和6 | ||
D、-
|
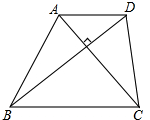 如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=BD.
如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=BD.