题目内容
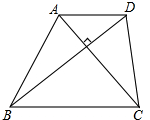如图，在四边形ABCD中，AD∥BC，且AD＜BC，AC、BD为两条对角线，且AC⊥BD，AC=BD．（1）按要求作图：把AC平移到DE的位置，方向为射线AD的方向，平移的距离为线段AD的长；
（2）判断△BDE的形状．
考点：作图-平移变换
专题：
分析：（1）延长BC至E，使CE=AD，连接DE即可；
（2）根据平移的性质可得DE∥AC，DE=AC，再根据两直线平行，内错角相等求出∠BDE=90°，然后根据等腰直角三角形的定义判定即可．
（2）根据平移的性质可得DE∥AC，DE=AC，再根据两直线平行，内错角相等求出∠BDE=90°，然后根据等腰直角三角形的定义判定即可．
解答：
解：（1）如图所示；
（2）由平移的性质得，DE∥AC，DE=AC，
∵AC=BD，
∴BD=DE，
∴△BDE是等腰直角三角形．
解：（1）如图所示；（2）由平移的性质得，DE∥AC，DE=AC，
∵AC=BD，
∴BD=DE，
∴△BDE是等腰直角三角形．
点评：本题考查了利用平移变换作图，等腰直角三角形的判定，熟练掌握平移的性质是解题的关键．
练习册系列答案
相关题目
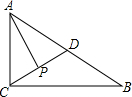△ABC中，AC=3，BC=4，AB=5，D是AB中点，点P由C沿CD方向运动，每秒钟移1个单位，若△APD的面积为y，点P移动时间为x秒，