题目内容
1.若a=1,b=2,则以a,b为边长的等腰三角形的周长为5.分析 题目给出等腰三角形有两条边长a=1,b=2,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解答 解:分两种情况考虑:
(1)如果腰长为1,则三边是:1、1、2,不满足三角形两边之和大于第三边的性质,不成立;
(2)如果腰长为2,则三边是:2、2、1,满足三角形两边之和大于第三边的性质,成立,故周长=2+2+1=5.
所以以a,b为边长的等腰三角形的周长为5.
故答案为:5.
点评 本题考查了等腰三角形的性质及三角形三边关系;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.

练习册系列答案
相关题目
12.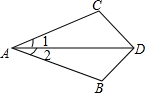 如图,已知∠1=∠2,欲得到△ABD≌△ACD,则从下列条件中补选一个,错误的选法是( )
如图,已知∠1=∠2,欲得到△ABD≌△ACD,则从下列条件中补选一个,错误的选法是( )
 如图,已知∠1=∠2,欲得到△ABD≌△ACD,则从下列条件中补选一个,错误的选法是( )
如图,已知∠1=∠2,欲得到△ABD≌△ACD,则从下列条件中补选一个,错误的选法是( )| A. | ∠ADB=∠ADC | B. | DB=DC | C. | ∠B=∠C | D. | AB=AC |
16.下列计算正确的是( )
| A. | x2•x4=x6 | B. | x2+x3=x5 | C. | (x2)3=x5 | D. | x10÷x2=x5 |
 如图,O是等边△ABC内的一点,已知∠AOB=110°,∠COD=60°,∠BOC=α,△BOC≌△ADC.
如图,O是等边△ABC内的一点,已知∠AOB=110°,∠COD=60°,∠BOC=α,△BOC≌△ADC.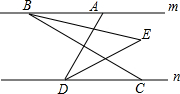 如图,已知直线m∥n,A、B是直线m上的任意两点,C、D是直线n上的任意两点,连AD、BC,∠ABC与∠ADC的平分线相交于点E,若∠BAD=80°.
如图,已知直线m∥n,A、B是直线m上的任意两点,C、D是直线n上的任意两点,连AD、BC,∠ABC与∠ADC的平分线相交于点E,若∠BAD=80°.