题目内容
现有一根长为64cm的铁丝
(1)若把该铁丝剪成两段,且每段均折成正方形,已知两个正方形面积的和等于160cm2,求两个正方形的边长;
(2)若把该铁丝剪成三段,且其中只有两段长度相同,并把每段均折成正方形,已知三个正方形面积的和等于152cm2,求这三个正方形的边长.
(1)若把该铁丝剪成两段,且每段均折成正方形,已知两个正方形面积的和等于160cm2,求两个正方形的边长;
(2)若把该铁丝剪成三段,且其中只有两段长度相同,并把每段均折成正方形,已知三个正方形面积的和等于152cm2,求这三个正方形的边长.
考点:一元二次方程的应用
专题:几何图形问题
分析:(1)设其中一个正方形的边长为xcm,则另一个正方形的边长为
cm,又因两个正方形的面积和等于160cm2,则可列出方程求解即可.
(2)设其中两个正方形的边长为xcm,则另一个正方形的边长为
cm,又因三个正方形的面积和等于152cm2,则可列出方程求解即可.
| 64-4x |
| 4 |
(2)设其中两个正方形的边长为xcm,则另一个正方形的边长为
| 64-8x |
| 4 |
解答:解:(1)设一个正方形的边长为xcm,
∵正方形的四边相等,
∴此正方形的周长是4xcm,另一个正方形的边长是
cm,
根据题意得x2+(
)2=160,
解得x1=12,x2=4.
当x=12时,
=4;
当x=4时,
=12,
所以两个正方形的边长为4cm或12cm.
(2)设其中两个正方形的边长为xcm,则另一个正方形的边长为
cm,
根据题意得到:2x2+(
)2=152,
解得:x1=2,x2=
;
则当x=2时,
=12;
当x=
时,
<0,所以不存在.
所以这三个正方形的边长分别为2cm、2cm、12cm.
∵正方形的四边相等,
∴此正方形的周长是4xcm,另一个正方形的边长是
| 64-4x |
| 4 |
根据题意得x2+(
| 64-4x |
| 4 |
解得x1=12,x2=4.
当x=12时,
| 64-4x |
| 4 |
当x=4时,
| 64-4x |
| 4 |
所以两个正方形的边长为4cm或12cm.
(2)设其中两个正方形的边长为xcm,则另一个正方形的边长为
| 64-8x |
| 4 |
根据题意得到:2x2+(
| 64-8x |
| 4 |
解得:x1=2,x2=
| 26 |
| 3 |
则当x=2时,
| 64-8x |
| 4 |
当x=
| 26 |
| 3 |
| 64-8x |
| 4 |
所以这三个正方形的边长分别为2cm、2cm、12cm.
点评:此题考查一元二次方程的实际运用,结合图形的周长和面积建立方程解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知:如图,AB∥DE,点F,点C在AD上,AF=DC,∠B=∠E.试说明:BC=EF.
已知:如图,AB∥DE,点F,点C在AD上,AF=DC,∠B=∠E.试说明:BC=EF. 用反证法证明:如图,已知AE、BF是平行四边形ABCD的两条高,且AE≠BF,求证:平行四边形ABCD不是菱形.
用反证法证明:如图,已知AE、BF是平行四边形ABCD的两条高,且AE≠BF,求证:平行四边形ABCD不是菱形.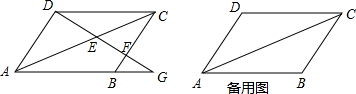
 如图,△ABC中,BC=6,AB=4,若△ABC的面积为9,则sinB=
如图,△ABC中,BC=6,AB=4,若△ABC的面积为9,则sinB=