题目内容
3月17日,新成立的中国铁路总公司已在北京正式挂牌,这标志着今后铁路将会进行一系列的客票改革.现某市铁路局拟实施淡季火车票打折销售制度.已知某班次列车一节车厢定员120人,原定票价为100元/人,淡季时上座率仅为20%.据调查,该列车票价每降低5元,单节车厢乘客人数将增加6人.
(1)该列车票价打几折时,单节车厢售票收入为4200元;
(2)该列车票价打几折时,单节车厢售票收入最高,并求出这个最高值.
(1)该列车票价打几折时,单节车厢售票收入为4200元;
(2)该列车票价打几折时,单节车厢售票收入最高,并求出这个最高值.
考点:一元二次方程的应用,二次函数的应用
专题:销售问题
分析:(1)由每降5元人数增加6人,设降价n个5元后的票价为(100-5n)元,则乘客人数为120×20%+6n=(24+6n),根据乘客人数×票数=售票收入列出方程求解;
(2)由(1)建立二次函数,利用配方法求最值即可.
(2)由(1)建立二次函数,利用配方法求最值即可.
解答:解:(1)设降价n个5元,根据题意得:
(100-5n)(24+6n)=4200
整理得-30n2+480n-1800=0
解得:x=10或x=6,
100-5n=50或70,
也就是打五折或打七折.
答:打五折或打七折时,单节车厢售票收入为4200元;
(2)y=(100-5n)(24+6n)
=-30n2+480n+2400
=-30(n-8)2+4320,
则当n=8时,y有最大值=4320,
即票价为100-5×8=60元,
也就是打6折.
答:该列车票价打六折时,单节车厢售票收入最高,最高4320元.
(100-5n)(24+6n)=4200
整理得-30n2+480n-1800=0
解得:x=10或x=6,
100-5n=50或70,
也就是打五折或打七折.
答:打五折或打七折时,单节车厢售票收入为4200元;
(2)y=(100-5n)(24+6n)
=-30n2+480n+2400
=-30(n-8)2+4320,
则当n=8时,y有最大值=4320,
即票价为100-5×8=60元,
也就是打6折.
答:该列车票价打六折时,单节车厢售票收入最高,最高4320元.
点评:此题考查一元二次方程的实际运用以及利用二次函数的性质求最大值的问题,找出题目蕴含的数量关系是解决问题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目

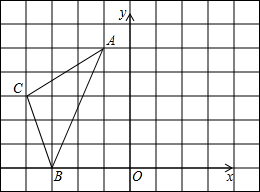 如图,在直角坐标系xOy中,A(-l,5),B(-3,0),C(-4,3).
如图,在直角坐标系xOy中,A(-l,5),B(-3,0),C(-4,3).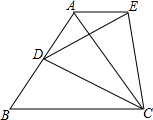 如图,在等边△ABC的边AB上任意取一点D,作等边△CDE.
如图,在等边△ABC的边AB上任意取一点D,作等边△CDE.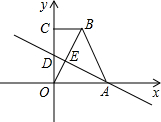 如图,四边形OABC中,CB∥OA,∠OCB=90?,CB=1,OA=OC,O为坐标原点,点A在x轴上,点C在y轴上,直线
如图,四边形OABC中,CB∥OA,∠OCB=90?,CB=1,OA=OC,O为坐标原点,点A在x轴上,点C在y轴上,直线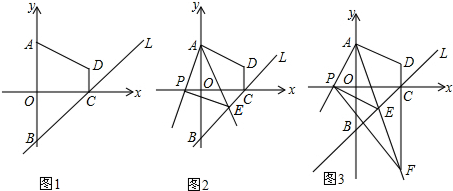
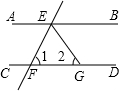 如图:AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2等于多少度?
如图:AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2等于多少度?