题目内容
18.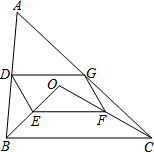 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.(1)求证:四边形DEFG是平行四边形;
(2)如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.
分析 (1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DG∥BC,DG=$\frac{1}{2}$BC,EF∥BC,EF=$\frac{1}{2}$BC,从而得到DG∥EF,DG=EF,然后根据一组对边平行且相等的四边形是平行四边形证明即可;
(2)过点O作OM⊥BC于M,由含30°的直角三角形的性质和等腰直角三角形的性质求得结果.
解答 证明:∵AB、OB、OC、AC的中点分别为D、E、F、G,
∴DG∥BC,DG=$\frac{1}{2}$BC,EF∥BC,EF=$\frac{1}{2}$BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:过点O作OM⊥BC于M,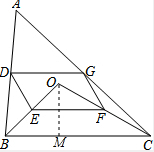
Rt△OCM中,∠OCM=30°,OC=4
∴OM=$\frac{1}{2}$OC=2,
∴CM=2$\sqrt{3}$,
Rt△OBM中,∠OBM=∠BOM=45°,
∴BM=OM=2,
∴BC=2+2$\sqrt{3}$,
∴EF=1+$\sqrt{3}$.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,含30°角,等腰直角三角形的性质,直角三角形的性质,熟记定理是解题的关键.

练习册系列答案
相关题目
9.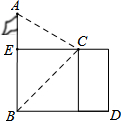 如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么,旗杆AB的高度是( )
如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么,旗杆AB的高度是( )
 如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么,旗杆AB的高度是( )
如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么,旗杆AB的高度是( )| A. | ($\sqrt{2}$+8$\sqrt{3}$)m | B. | (8+8$\sqrt{3}$)m | C. | (8$\sqrt{2}$+$\frac{8\sqrt{3}}{3}$)m | D. | (8+$\frac{8\sqrt{3}}{3}$)m |
6.在下列交通标志中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.一次数学单元测试中,初三(1)班第一小组的10个学生的成绩分别是:58分、72分、76分、82分、82分、89分、91分、91分、91分、98分,那么这次测试第一小组10个学生成绩的众数和平均数分别是( )
| A. | 82分、83分 | B. | 83分、89分 | C. | 91分、72分 | D. | 91分、83分 |
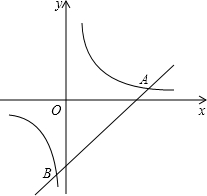 如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点.
如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点. 如图,△ABC中,∠ACB=90°,延长AC到D,使得CD=CB,过点D作DE⊥AB于点E,交BC于F.求证:AB=DF.
如图,△ABC中,∠ACB=90°,延长AC到D,使得CD=CB,过点D作DE⊥AB于点E,交BC于F.求证:AB=DF.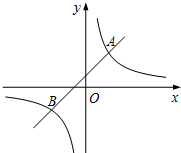 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.