题目内容
1．
解不等式2（x+4）-5＜3（x+1）+4，并把解集在如图所示的数轴上表示出来．
分析 利用解不等式的步骤，一步步得出结论，再利用数轴标根法将不等式的值域在数轴上表示出来．
解答 解：2（x+4）-5＜3（x+1）+4，
展开移项得：8-5-3-4＜3x-2x，
合并同类项得：-4＜x．
故不等式的解集为：x＞-4．
将解集在数轴上表示如下．
点评 本题考查了解一元一次不等式以及在数轴上表示不等式的解集，解题的关键是牢记解不等式的步骤．本题属于基础题，难度不大，只需熟悉不等式的解法即可解决该类题型．
练习册系列答案
相关题目
11．下列运算正确的是（ ）
| A． | $\sqrt{4}=±2$ | B． | |-2|=-2 | C． | -22=4 | D． | $-\sqrt{4}=-2$ |
已知，在△ABC中∠ACB=90°，AC=BC，点P在△ABC内，且PA=3，PB=1，PC=2，求证：∠BPC=135°．
9．若点（-1，y1），（-2，y2），（2，y3）在反比例函数$y=-\frac{{{k^2}+1}}{x}$图象上，则下列结论正确的是（ ）
| A． | y1＞y2＞y3 | B． | y2＞y1＞y3 | C． | y3＞y1＞y2 | D． | y3＞y2＞y1 |
16．
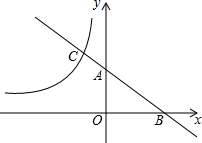如图，平面直角坐标系中，直线y=-x+a与x、y轴的正半轴分别交于点B和点A，与反比例函数y=-$\frac{3}{x}$的图象交于点C，若BA：AC=2：1，则a的值为（ ）
如图，平面直角坐标系中，直线y=-x+a与x、y轴的正半轴分别交于点B和点A，与反比例函数y=-$\frac{3}{x}$的图象交于点C，若BA：AC=2：1，则a的值为（ ）| A． | 2 | B． | -2 | C． | 3 | D． | -3 |
6．下列每组数分别是三根小木棒的长度（cm），用它们能摆成三角形的是（ ）
| A． | 3 4 9 | B． | 2 3 5 | C． | 5 12 13 | D． | 5 5 11 |