题目内容
3.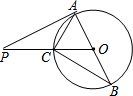 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于C,连结BC、AC,若∠PAC=30°,AC=4,则BC=4$\sqrt{3}$.
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于C,连结BC、AC,若∠PAC=30°,AC=4,则BC=4$\sqrt{3}$.
分析 由切线的性质易求∠CAO=60°,由圆周角定理可得△ACB是直角三角形,又因为AC的长已知,所以BC的长可求.
解答 解:
∵PA切⊙O于点A,
∴OA⊥AB,
∵∠PAC=30°,
∴∠CAO=60°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=4,
∴BC=$\sqrt{3}$AC=4$\sqrt{3}$,
故答案为:4$\sqrt{3}$.
点评 本题考查了切线的性质定理,熟练运用切线的性质定理和圆周角定理的推论是解题的关键.

练习册系列答案
相关题目
11.下列运算正确的是( )
| A. | $\sqrt{4}=±2$ | B. | |-2|=-2 | C. | -22=4 | D. | $-\sqrt{4}=-2$ |
15.已知圆锥的侧面积为6πcm2,侧面展开图的圆心角为60°,则该圆锥的母线长( )
| A. | 36cm | B. | 18cm | C. | 6cm | D. | 3cm |
 已知,在△ABC中∠ACB=90°,AC=BC,点P在△ABC内,且PA=3,PB=1,PC=2,求证:∠BPC=135°.
已知,在△ABC中∠ACB=90°,AC=BC,点P在△ABC内,且PA=3,PB=1,PC=2,求证:∠BPC=135°.