题目内容
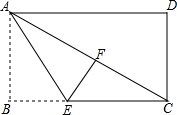如图，在长方形ABCD中，AB=6，BC=8，先将矩形沿对角线折叠，再将矩形沿AE对折，使点B落在AC边的点F处，求折痕AE的长．考点：翻折变换（折叠问题）
专题：
分析：利用勾股定理列式求出AC，设BE=x，表示出CE，根据翻折的性质可得BE=EF，AF=AB，再求出CF，然后利用勾股定理列方程求出x，再利用勾股定理列式计算即可得解．
解答：解：由勾股定理得，AC=
=
=10，
设BE=x，则CE=8-x，
由翻折的性质得，BE=EF=x，AF=AB=6，
所以，CF=10-6=4，
在Rt△CEF中，由勾股定理得，EF2+CF2=CE2，
即x2+42=（8-x）2，
解得x=3，
在Rt△ABE中，AE=
=
=3
，
即折痕AE的长是3
．
| AB2+BC2 |
| 62+82 |
设BE=x，则CE=8-x，
由翻折的性质得，BE=EF=x，AF=AB=6，
所以，CF=10-6=4，
在Rt△CEF中，由勾股定理得，EF2+CF2=CE2，
即x2+42=（8-x）2，
解得x=3，
在Rt△ABE中，AE=
| AB2+BE2 |
| 62+32 |
| 5 |
即折痕AE的长是3
| 5 |
点评：本题考查了翻折变换的性质，勾股定理，此类题目，熟记性质并利用勾股定理列出方程是解题的关键．
练习册系列答案
相关题目
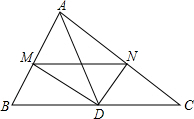在△ABC中，AD是中线，DM是∠ADB的平分线，交AB于M，DN是∠ADC的平分线交AC于N点．求证：BM+CN＞MN．
如图，AB为圆O的直径，C为圆O上一点，AD和过C点的直线互相垂直，垂足为D，且AC平分∠DAB，延长AB交DC于点E，CF⊥AB于点F．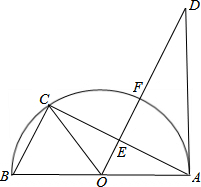
如图，AB是半圆O的直径，点C在半圆O上，过点O作OD∥BC交圆的切线AD于点D，交弦AC于E，交半圆于点F．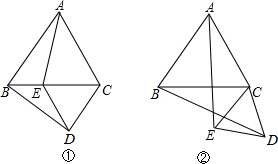
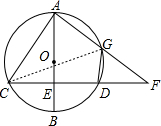已知如图，CF⊥AB，AB为直径，求证：AC•DG=AG•DF．