题目内容
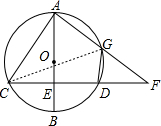已知如图，CF⊥AB，AB为直径，求证：AC•DG=AG•DF．考点：圆周角定理,相似三角形的判定与性质
专题：证明题
分析：如图，作辅助线，首先证明∠AGC=∠ACD，进而证明△ACG∽△DFG，列出比例式即可解决问题．
解答：证明：如图，连接CG；
∵CF⊥AB，AB为直径，
∴
=
，
∴∠AGC=∠ACD；
在△ACG与△DFG中，
，
∴△ACG∽△DFG，
∴
=
，
∴AC•DG=AG•DF．
证明：如图，连接CG；∵CF⊥AB，AB为直径，
∴
 |
| AC |
|
| AGD |
∴∠AGC=∠ACD；
在△ACG与△DFG中，
|
∴△ACG∽△DFG，
∴
| AC |
| DF |
| AG |
| DG |
∴AC•DG=AG•DF．
点评：该题主要考查了垂径定理、相似三角形的判定及其性质的应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
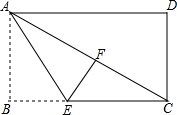如图，在长方形ABCD中，AB=6，BC=8，先将矩形沿对角线折叠，再将矩形沿AE对折，使点B落在AC边的点F处，求折痕AE的长．
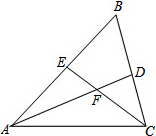如图，在△ABC中，∠B=60°，AD、CE分别是∠BAC、∠ACB的角平分线，AD、CE相交于F．已知点A的坐标为（3，4），O为原点，连结OA，将线段OA绕点O按逆时针方向旋转90°得OA1，则点A1的坐标为（ ）
| A、（-3，4） |
| B、（3，-4） |
| C、（-4，3） |
| D、（4，-3） |
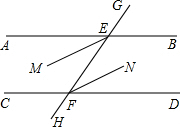如图，已知直线AB和直线CD被直线GH所截，交点分别为E，F，∠AEF=∠EFD．