题目内容
如图,在矩形ABCD中,AB<BC,AC,BD交于点O.点E为线段AC上的一个动点,连接DE,BE,过E作EF⊥BD于F,设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
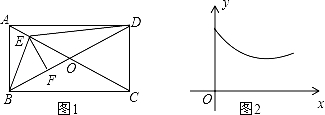
A.线段EF B.线段DE C.线段CE D.线段BE
B【考点】动点问题的函数图象.
【分析】作BN⊥AC,垂足为N,FM⊥AC,垂足为M,DG⊥AC,垂足为G,分别找出线段EF、CE、BE最小值出现的时刻即可得出结论.
【解答】解:作BN⊥AC,垂足为N,FM⊥AC,垂足为M,DG⊥AC,垂足为G.

由垂线段最短可知:当点E与点M重合时,即AE< 时,FE有最小值,与函数图象不符,故A错误;
时,FE有最小值,与函数图象不符,故A错误;
由垂线段最短可知:当点E与点G重合时,即AEd> 时,DE有最小值,故B正确;
时,DE有最小值,故B正确;
∵CE=AC﹣AE,CE随着AE的增大而减小,故C错误;
由垂线段最短可知:当点E与点N重合时,即AE< 时,BE有最小值,与函数图象不符,故D错误;
时,BE有最小值,与函数图象不符,故D错误;
故选:B.
【点评】本题主要考查的是动点问题的函数图象,根据垂线段最短确定出函数最小值出现的时刻是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 +
+
 =2;
=2;  ,则2xy的值为( )
,则2xy的值为( ) D.
D.

 在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是 .
在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是 .
 ,求线段CD的长.
,求线段CD的长.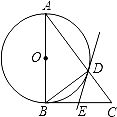

 B.
B.
