题目内容
济宁市“五城同创”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了x天完成,乙做另一部分用了y天完成,其中x、y均为正整数,且x<46,y<52,求甲、乙两队各做了多少天?
【考点】分式方程的应用;一元一次不等式组的应用.
【专题】工程问题.
【分析】(1)设乙工程队单独完成这项工作需要a天,由题意列出分式方程,求出a的值即可;
(2)首先根据题意列出x和y的关系式,进而求出x的取值范围,结合x和y都是正整数,即可求出x和y的值.
【解答】解:(1)设乙工程队单独完成这项工作需要a天,由题意得
 +36(
+36( )=1,
)=1,
解之得a=80,
经检验a=80是原方程的解.
答:乙工程队单独做需要80天完成;
(2)∵甲队做其中一部分用了x天,乙队做另一部分用了y天,
∴ =1
=1
即y=80﹣ x,
x,
又∵x<46,y<52,
∴ ,
,
解得42<x<46,
∵x、y均为正整数,
∴x=45,y=50,
答:甲队做了45天,乙队做了50天.
【点评】本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.此题涉及的公式:工作总量=工作效率×工作时间.

练习册系列答案
相关题目

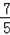

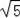
 B.5 C.
B.5 C.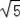
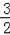


 ,则
,则 =__________.
=__________. |+
|+ ﹣(3.14﹣π)0﹣(﹣
﹣(3.14﹣π)0﹣(﹣ )﹣1.
)﹣1. 偶数号各3个.若小丁从中随机抽取一个,则抽到的座位号是偶数的概率是( )
偶数号各3个.若小丁从中随机抽取一个,则抽到的座位号是偶数的概率是( ) B.
B. C.
C.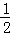 D.
D.
 的两根,则这个三角形的周长为( )
的两根,则这个三角形的周长为( )