题目内容
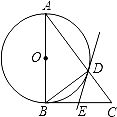
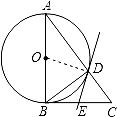
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与边AC交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)证明:DE是⊙O的切线;
(2)若⊙O的半径R=5,tanA=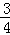 ,求线段CD的长.
,求线段CD的长.
【考点】切线的判定.
【分析】(1)首先连接OD,由∠BDE=∠A,易得∠ODA=∠BDE,又由AB为直径,可得∠ADB=90°,继而求得∠ODE=90°,则可证得:DE是⊙O的切线.
(2)在Rt△ABC中,可得tanA=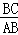 =
=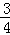 ,则可求得BC的长,然后由勾股定理求得AC的长,易证得△BCD∽△ACB,然后由相似三角形的对应边成比例,求得答案.
,则可求得BC的长,然后由勾股定理求得AC的长,易证得△BCD∽△ACB,然后由相似三角形的对应边成比例,求得答案.
【解答】(1)证明:连接OD.
∵OA=OD,
∴∠ODA=∠A.
又∵∠BDE=∠A,
∴∠ODA=∠BDE.
∵AB是⊙O直径,
∴∠ADB=90°.
即∠ODA+∠ODB=90°.
∴∠BDE+∠ODB=90°.
∴∠ODE=90°.
∴DE是⊙O的切线.
(2)解:∵R=5,
∴AB=10.
在Rt△ABC中,
∵tanA=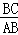 =
=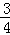 ,
,
∴BC=AB•tanA=10×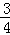 =
=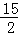 ,
,
∴AC=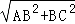 =
=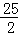 ,
,
∵∠BDC=∠ABC=90°,∠BCD=∠ACB,
∴△BCD∽△ACB.
∴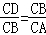 ,
,
∴CD=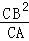 =
=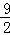 .
.
【点评】此题考查了切线的性质与判定、勾股定理以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目

 |+
|+ ﹣(3.14﹣π)0﹣(﹣
﹣(3.14﹣π)0﹣(﹣ )﹣1.
)﹣1.
 B于P.若CG=3.则△CGE与四边形BFHP的面积之和为 .
B于P.若CG=3.则△CGE与四边形BFHP的面积之和为 .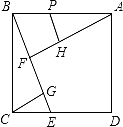
 的两根,则这个三角形的周长为( )
的两根,则这个三角形的周长为( ) 对应的图象为( )
对应的图象为( ) B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.

 x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=
x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=