题目内容
6.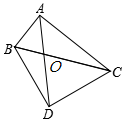 如图,在四边形ABDC中,对角线AD、BC交于点O,∠BAC=90°,∠BDC=90°,BD=CD,AB=2,AC=4,记△AOC的面积为S1、△BOD的面积为S2,则S1-S2的值为( )
如图,在四边形ABDC中,对角线AD、BC交于点O,∠BAC=90°,∠BDC=90°,BD=CD,AB=2,AC=4,记△AOC的面积为S1、△BOD的面积为S2,则S1-S2的值为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
分析 如图,作DE⊥AC于E,DF⊥AB于F则四边形AFDE是矩形.只要证明△DFB≌△DEC,可得DE=DF,BF=CE,推出AB+AC=AF-BF+AE+CE=2AE=6,推出AE=AF=3,根据S1-S2=S△ABC-S△ABD计算即可.
解答 解:如图,作DE⊥AC于E,DF⊥AB于F则四边形AFDE是矩形.
∴∠EDF=∠BDC=90°,
∴∠BDF=∠EDC,∵∠F=∠DEC=90°,DB=DC,
∴△DFB≌△DEC,
∴DE=DF,BF=CE,
∴AB+AC=AF-BF+AE+CE=2AE=6,
∴AE=AF=3,
∵S1-S2=S△ABC-S△ABD=$\frac{1}{2}$•2•4-$\frac{1}{2}$•2•3=1,
故选A.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、三角形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.如果a=b,则下列式子不一定成立的是( )
| A. | a+1=b+1 | B. | $\frac{a}{3}$=$\frac{b}{3}$ | C. | a2=b2 | D. | a-c=c-b |
17.已知双曲线y=$\frac{k}{x}$上有一点P(2,-3),则点A(6,1)、B(-2,3)、C($\frac{1}{2}$,-12)、D(-7,1)中,在该双曲线上的还有( )
| A. | 点A、B | B. | 点A、C | C. | 点B、C | D. | 点B、D |
14.计算:($\frac{4}{5}$)2014×($\frac{5}{4}$)2015的结果是( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | ($\frac{4}{5}$)4029 | D. | ($\frac{5}{4}$)2029 |
1.下列运算正确的是( )
| A. | (a+b)(a-b)=a2-b2 | B. | (2a2)3=6a6 | C. | a6÷a2=a3 | D. | -1-1=0 |
11.以下列各组数据为边长,能构成三角形的是( )
| A. | 4,4,8 | B. | 2,4,7 | C. | 4,8,8 | D. | 2,2,7 |
18.在-1、-|-3|、-(-2)、1这四个数中最大的数是( )
| A. | -1 | B. | -|-3| | C. | -(-2) | D. | 1 |
