题目内容
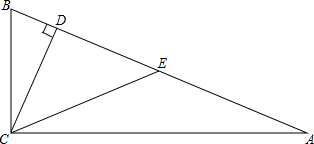 在Rt△ABC中,∠ACB=90°,CD⊥AB,CE为AB边上的中线,∠ACD=3∠BCD.求证:DE=DC.
在Rt△ABC中,∠ACB=90°,CD⊥AB,CE为AB边上的中线,∠ACD=3∠BCD.求证:DE=DC.考点:直角三角形斜边上的中线
专题:
分析:先求出∠BCD,再根据直角三角形两锐角互余求出∠B,然后根据直角三角形斜边上的中线等于斜边的一半可得CE=BE,根据等边对等角可得∠BCE=∠B,再求出∠DCE=45°,然后判断出△CDE是等腰直角三角形,最后根据等腰直角三角形的性质证明即可.
解答:
证明:∵∠ACB=90°,∠ACD=3∠BCD,
∴∠BCD=90°×
=22.5°,
∵CD⊥AB,
∴∠B=90°-∠BCD=90°-22.5°=67.5°,
∵∠ACB=90°,CE为AB边上的中线,
∴CE=BE,
∴∠BCE=∠B=67.5°,
∴∠DCE=∠BCE-∠BCD=67.5°-22.5°=45°,
又∵CD⊥AB,
∴△CDE是等腰直角三角形,
∴DE=DC.
∴∠BCD=90°×
| 1 |
| 1+3 |
∵CD⊥AB,
∴∠B=90°-∠BCD=90°-22.5°=67.5°,
∵∠ACB=90°,CE为AB边上的中线,
∴CE=BE,
∴∠BCE=∠B=67.5°,
∴∠DCE=∠BCE-∠BCD=67.5°-22.5°=45°,
又∵CD⊥AB,
∴△CDE是等腰直角三角形,
∴DE=DC.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等边对等角的性质,等腰直角三角形的判定与性质,熟记各性质并求出∠DCE=45°是解题的关键.

练习册系列答案
相关题目
已知弦AB把圆周分成1:5的两部分,则弦AB所对应的圆周角的度数为( )
| A、30° |
| B、30°或150° |
| C、60° |
| D、60°或300° |
 如图,是用两个同样大小的长方体搭成的几何体,这个几何体的左视图是( )
如图,是用两个同样大小的长方体搭成的几何体,这个几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
 某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构,根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构,根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示: 如图,为了测量山AB的高度,先在山脚的一点C测得山顶A的仰角为45°,再沿坡角为15°的山坡走100米到点D,又测得山顶A的仰角是75°,则山高AB=
如图,为了测量山AB的高度,先在山脚的一点C测得山顶A的仰角为45°,再沿坡角为15°的山坡走100米到点D,又测得山顶A的仰角是75°,则山高AB= 如图,一颗高6m的树在太阳光的照射下,影长为10m,求此时太阳光线与地面所成角的正切值.
如图,一颗高6m的树在太阳光的照射下,影长为10m,求此时太阳光线与地面所成角的正切值.