题目内容
 如图,为了测量山AB的高度,先在山脚的一点C测得山顶A的仰角为45°,再沿坡角为15°的山坡走100米到点D,又测得山顶A的仰角是75°,则山高AB=
如图,为了测量山AB的高度,先在山脚的一点C测得山顶A的仰角为45°,再沿坡角为15°的山坡走100米到点D,又测得山顶A的仰角是75°,则山高AB=考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:延长AD交CB于点G,过点D作DM⊥AC于点M,先求出∠CAG=30°,∠ACD=30°,得出AM=CM,在Rt△CDM中,根据cos∠DCM=
,求出CM,得出AC=2CM=100
,在Rt△ABC中,根据AB=sin∠ACB•AC,代入计算即可.
| CM |
| CD |
| 3 |
解答:
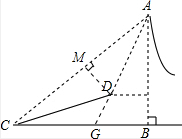 解:延长AD交CB于点G,过点D作DM⊥AC于点M,
解:延长AD交CB于点G,过点D作DM⊥AC于点M,
则∠AGB=75°,
∵∠ACB=45°,
∴∠CAG=30°,
∵∠DCG=15°,
∴∠ACD=30°,
∴AD=CD,
∴AM=CM,
在Rt△CDM中,
∵cos∠DCM=
,
∴CM=cos∠DCM•CD=cos30°×100=50
,
∴AC=100
,
在Rt△ABC中,
∵sin∠ACB=
,
∴AB=sin∠ACB•AC=sin45°×100
=
×100
=50
.
 解:延长AD交CB于点G,过点D作DM⊥AC于点M,
解:延长AD交CB于点G,过点D作DM⊥AC于点M,则∠AGB=75°,
∵∠ACB=45°,
∴∠CAG=30°,
∵∠DCG=15°,
∴∠ACD=30°,
∴AD=CD,
∴AM=CM,
在Rt△CDM中,
∵cos∠DCM=
| CM |
| CD |
∴CM=cos∠DCM•CD=cos30°×100=50
| 3 |
∴AC=100
| 3 |
在Rt△ABC中,
∵sin∠ACB=
| AB |
| AC |
∴AB=sin∠ACB•AC=sin45°×100
| 3 |
| ||
| 2 |
| 3 |
| 6 |
点评:本题考查了解直角三角形的应用,用到的知识点是特殊角的三角函数值、仰角的定义等知识点,要求学生能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各式从左到右的变化属于因式分解的是( )
| A、m2-4n2=(m+2n)(m-2n) |
| B、(m+1)(m-1)=m2-1 |
| C、m2-2m-4=m(m-2)-4 |
| D、m2-2m-3=(m-1)2-4 |
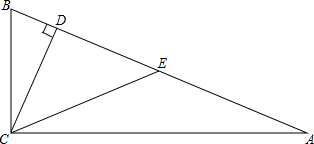 在Rt△ABC中,∠ACB=90°,CD⊥AB,CE为AB边上的中线,∠ACD=3∠BCD.求证:DE=DC.
在Rt△ABC中,∠ACB=90°,CD⊥AB,CE为AB边上的中线,∠ACD=3∠BCD.求证:DE=DC. 如图,在矩形ABCD中,AE=2ED,BF=2FC,AD=3cm.若矩形AEFB与矩形ABCD相似,则AB=
如图,在矩形ABCD中,AE=2ED,BF=2FC,AD=3cm.若矩形AEFB与矩形ABCD相似,则AB= 如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为点A、B.
如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为点A、B. 已知,如图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其B,C,D点的坐标分别为(1,2),(1,1),(3,1).
已知,如图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其B,C,D点的坐标分别为(1,2),(1,1),(3,1).