题目内容
 数学课老师提出这样一个问题:已知如图,直线AB∥CD,直线EF与直线AB交于G,与直线CD交于H,且GN平分∠EGB,求证:∠4=
数学课老师提出这样一个问题:已知如图,直线AB∥CD,直线EF与直线AB交于G,与直线CD交于H,且GN平分∠EGB,求证:∠4=| 1 |
| 2 |
下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整.
证明:
∵CD与EF相交于点H,(已知)
∴∠1=∠2(
∵AB∥CD,EF与AB、CD分别交于G、H(已知)
∴∠2=∠EGB(
∵GN是∠EGB的平分线,(已知)
∴∠4=
∵∠1=∠2,∠2=∠EGB(已证)
∴∠1=∠EGB(
∵
∴∠4=
| 1 |
| 2 |
考点:平行线的性质
专题:推理填空题
分析:先根据对顶角的性质得出∠1=∠2,再根据AB∥CD,得出∠2=∠EGB,由GN是∠EGB的平分线,可知∠4=
∠EGB,故可得出∠1=∠EGB,由此可得出结论.
| 1 |
| 2 |
解答:证明:∵CD与EF相交于点H,
∴∠1=∠2.
∵AB∥CD,EF与AB、CD分别交于G、H,
∴∠2=∠EGB.
∵GN是∠EGB的平分线,
∴∠4=
∠EGB.
∵∠1=∠2,∠2=∠EGB(已证),
∴∠1=∠EGB.
∵∠4=
∠EGB,
∴∠4=
∠1.
故答案为:对顶角的性质,两直线平行,同位角相等,
,等量代换,∠4=
∠EGB.
∴∠1=∠2.
∵AB∥CD,EF与AB、CD分别交于G、H,
∴∠2=∠EGB.
∵GN是∠EGB的平分线,
∴∠4=
| 1 |
| 2 |
∵∠1=∠2,∠2=∠EGB(已证),
∴∠1=∠EGB.
∵∠4=
| 1 |
| 2 |
∴∠4=
| 1 |
| 2 |
故答案为:对顶角的性质,两直线平行,同位角相等,
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列数中最小的是( )
| A、3 | B、2 | C、-1 | D、0 |
 已知△ABC中,∠A=25°,∠B=40°.
已知△ABC中,∠A=25°,∠B=40°.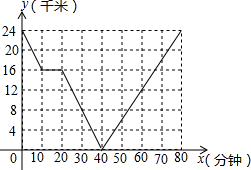 现有一直线型道路连接甲、乙两地,小文骑车从甲地出发到乙地后立即又按原路赶回甲地.已知他离乙地的距离y(千米)与骑车的时问x(分钟)之间的函数关系的图象如图所示.
现有一直线型道路连接甲、乙两地,小文骑车从甲地出发到乙地后立即又按原路赶回甲地.已知他离乙地的距离y(千米)与骑车的时问x(分钟)之间的函数关系的图象如图所示.