题目内容
11.若-a|x-1|b2与$\frac{1}{2}$a2b|y+2|可以合并,则x=3或-1,y=0或-4.分析 首先判断单项式-a|x-1|b2与$\frac{1}{2}$a2b|y+2|是同类项,再由同类项的定义,可得出x、y的值.
解答 解:∵-a|x-1|b2与$\frac{1}{2}$a2b|y+2|可以合并,
∴-a|x-1|b2与$\frac{1}{2}$a2b|y+2|是同类项,
∴|x-1|=2,|y+2|=2,
∴x=3或-1,y=0或-4,
故答案为:3或-1,0或-4.
点评 本题考查了同类项的知识,属于基础题,解答本题的关键是掌握同类项中的两个相同.

练习册系列答案
相关题目
6.下列去(添)括号正确做法的有( )
| A. | x-(y-x)=x-y-z | B. | -(x-y+z)=-x-y-z | ||
| C. | x+2y-2z=x-2(y-z) | D. | -a+c+d+b=-(a-b)+(c+d) |
3.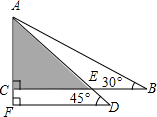 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.| A. | 14 | B. | 24.5 | C. | 7 | D. | 49 |
 已知P(-3,m)和 Q(1,m)是抛物线y=x2+bx-3上的两点.
已知P(-3,m)和 Q(1,m)是抛物线y=x2+bx-3上的两点.