题目内容
7.(1)已知2a=5b=10,求$\frac{1}{a}$+$\frac{1}{b}$的值.(2)已知2a=5b=10c,证明:ab=ac+bc.
分析 (1)根据积的乘方,可得2ab×5ab=(2×5)ab=10,根据同底数幂的乘法,可得10a×10b=10a+b,根据等式的性质,可得答案.
(2)根据积的乘方,可得指数相同的幂的乘法,根据幂的乘方,可得同底数幂的乘法,根据同底数幂的乘法,可得相同的幂.根据同底数的幂相同,可得指数相同.
解答 解:(1)∵2a=10,
∴(2a)b=10b,2ab=10b①;
∵5b=10,
∴(5b)a=10a,5ab=10b②,
①×②,得
2ab×5ab=(2×5)ab=10ab,
10a×10b=10a+b,
ab=a+b,
两边都除以ab,
∴$\frac{1}{a}$+$\frac{1}{b}$=1;
(2)设2a=5b=10c=k,
则 10ab=2ab×5ab=(2a)b×(5b)a=kb•ka=ka+b,
10ac+bc=(10c)a+b=ka+b
所以 10ab=10ac+bc,
所以 ab=ac+bc.
点评 本题主要考查了幂的乘方与积得乘方,先由积的乘方化成同底数幂的乘法,再由幂的乘方化成同底数的相同的幂求出是解题关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
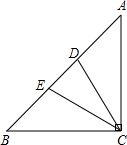 如图,在△ABC中,∠ACB=90°,∠A=45°,AC=AE,BC=BD.求证:△CDE是等腰三角形.
如图,在△ABC中,∠ACB=90°,∠A=45°,AC=AE,BC=BD.求证:△CDE是等腰三角形.