题目内容
 如图,在△ABC中,AE是BC边上的高,AD是角平分线,∠B=42°,∠C=68°,分别求∠BAC、∠DAE的度数.
如图,在△ABC中,AE是BC边上的高,AD是角平分线,∠B=42°,∠C=68°,分别求∠BAC、∠DAE的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:由三角形内角和定理可求得∠BAC的度数,在Rt△AEC中,可求得∠EAC的度数,AD是角平分线,有∠DAC=
∠BAC,故∠EAD=∠DAC-∠EAC.
| 1 |
| 2 |
解答:解:∵∠B=42°,∠C=68°,
∴∠BAC=180°-∠B-∠C=70°,
∵AD是角平分线,
∴∠EAC=
∠BAC=35°.
∵AE是高,∠C=68°,
∴∠DAC=90°-∠C=22°,
∴∠EAD=∠DAC-∠EAC=35°-22°=13°.
∴∠BAC=180°-∠B-∠C=70°,
∵AD是角平分线,
∴∠EAC=
| 1 |
| 2 |
∵AE是高,∠C=68°,
∴∠DAC=90°-∠C=22°,
∴∠EAD=∠DAC-∠EAC=35°-22°=13°.
点评:考查了三角形内角和定理,本题利用了三角形内角和定理、角的平分线的性质、直角三角形的性质求解.

练习册系列答案
相关题目
 如图,在直线MN上找点P,使点P到∠AOB两边的距离相等,符合条件的有( )个.
如图,在直线MN上找点P,使点P到∠AOB两边的距离相等,符合条件的有( )个.| A、0 | B、1 | C、2 | D、3 |
已知在△ABC中有两个角的大小分别为40°和70°,则这个三角形是( )
| A、直角三角形 |
| B、等边三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
 如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.
如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.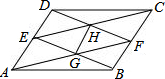 在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC.
在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC.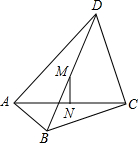 如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M、N分别是对角线BD、AC的中点.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M、N分别是对角线BD、AC的中点. 如图,已知平行四边形ABCD中,对角线AC和BD相交于点O.在BC上取点E,使EC=
如图,已知平行四边形ABCD中,对角线AC和BD相交于点O.在BC上取点E,使EC=