题目内容
4.某校组织275名师生到青少年活动中心参加劳技活动,计划租用甲、乙两种客车共7辆,已知甲种客车载客量是30人,乙种客车载客量是45人.其中,每辆乙种客车租金比甲种客车多100元,5辆甲种客车和2辆乙种客车租金共需2300元.(1)租用一辆甲种客车、一辆乙种客车各多少元?
(2)设租用甲种客车x辆,总租车费为w元,求w与x的函数关系;在保证275名师生都有座位的前提下,求当租用甲种客车多少辆时,总租车费最少,并求出这个最少费用.
分析 (1)设租用一辆甲种客车的费用为x元,则一辆乙种客车的费用为(x+100)元,列出方程即可解决问题;
(2)由题意w=300x+400(7-x)=-100x+2800,列出不等式求出x的取值范围,利用一次函数的性质即可解决问题.
解答 解:(1)设租用一辆甲种客车的费用为x元,则一辆乙种客车的费用为(x+100)元,
由题意5x+2(x+100)=2300,
解得x=300,
答:租用一辆甲种客车的费用为300元,则一辆乙种客车的费用为400元.
(2)由题意w=300x+400(7-x)=-100x+2800,
又30x+45(7-x)≥275,
解得x≤$\frac{8}{3}$,
∴x的最大值为2,
∵-100<0,
∴x=2时,w的值最小,最小值为2600.
答:当租用甲种客车2辆时,总租车费最少,最少费用为2600元.
点评 本题考查一元一次方程的应用、一次函数的应用、一元一次不等式的应用等知识,解题的关键是理解题意,学会构建一次函数解决最值问题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
15.下列各式属于最简二次根式的是( )
| A. | $\sqrt{0.1}$ | B. | $\sqrt{8}$ | C. | $\sqrt{{x^2}+{x^2}y}$ | D. | $\sqrt{{x^2}+1}$ |
19.一正方形面积为27,则它的边长为( )
| A. | 在3到4之间 | B. | 在4到5之间 | C. | 在5到6之间 | D. | 在6到7之间 |
14.若代数式mx2+2(3-2m)x+1(m≠0)是关于x的完全平方式,则m等于( )
| A. | 1 | B. | -1 | C. | 1或$\frac{9}{4}$ | D. | -1或-$\frac{9}{4}$ |
 如图,求∠A+∠B+∠C+∠D+∠E+∠F的值.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的值.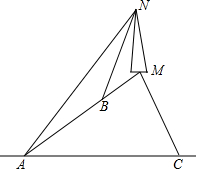 如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:
如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求: