题目内容
20.满足下列条件的△ABC,是直角三角形的有( )个.(1)∠A-∠B=∠C
(2)∠A:∠B:∠C=3:4:5
(3)∠A=2∠B=3∠C
(4)a=20,b=21,c=29
(5)a=7,b=8,c=10
(6)a=2,b=$\sqrt{3}$,c=$\sqrt{7}$(其中∠A、∠B、∠C是△ABC的三个内角,a,b,c是△ABC的三条边)
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 (1)根据∠A、∠B、∠C之间的关系结合三角形内角和定理即可得出∠A=90°,由此得出条件(1)符合题意;(2)根据∠A、∠B、∠C之间的关系结合三角形内角和定理即可得出∠A=45°、∠B=60°、∠C=75°,由此得出条件(2)不符合题意;(3)根据∠A、∠B、∠C之间的关系结合三角形内角和定理即可得出∠A=$\frac{1080}{11}$°、∠B=$\frac{540}{11}$°、∠C=$\frac{360}{11}$°,由此得出条件(3)不符合题意;(4)根据a、b、c的值即可得出a2+b2=841=c2,由此得出条件(4)符合题意;(5)根据a、b、c的值即可得出a2+b2=113>100=c2,由此可得出△ABC为锐角三角形,即条件(5)不符合题意;(6)根据a、b、c的值即可得出a2+b2=7=c2,由此得出条件(6)符合题意.
解答 解:(1)∵∠A-∠B=∠C,∠A+∠B+∠C=180°,
∴∠A=∠B+∠C=180°÷2=90°,
∴△ABC为直角三角形,
∴条件(1)满足题意;
(2)∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,
∴∠A=45°,∠B=60°,∠C=75°,
∴△ABC为锐角三角形,
∴条件(2)不符合题意;
(3)∵∠A=2∠B=3∠C,∠A+∠B+∠C=180°,
∴∠A=$\frac{1080}{11}$°,∠B=$\frac{540}{11}$°,∠C=$\frac{360}{11}$°,
∴△ABC为钝角三角形,
∴条件(3)不符合题意;
(4)∵a=20,b=21,c=29,
∴a2+b2=841=c2,
∴△ABC为直角三角形,
∴条件(4)符合题意;
(5)∵a=7,b=8,c=10,
∴a2+b2=113>100=c2,
∴△ABC为锐角三角形,
∴条件(5)不符合题意;
(6)∵a=2,b=$\sqrt{3}$,c=$\sqrt{7}$,
∴a2+b2=7=c2,
∴△ABC为直角三角形,
∴条件(6)符合题意.
综上所述:符合题意的有(1)(4)(6).
故选B.
点评 本题考查了勾股定理的逆定理以及三角形内角和定理,逐一分析6个条件是否满足△ABC为直角三角形是解题的关键.

 阅读快车系列答案
阅读快车系列答案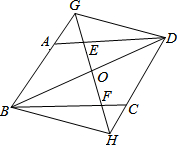 如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连结GD、BH,则下列结论:①AG=CH,②DE+CF=5,③S四边形ABFE=3$\sqrt{3}$,④四边形BGDH为平行四边形.其中正确的有( )
如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连结GD、BH,则下列结论:①AG=CH,②DE+CF=5,③S四边形ABFE=3$\sqrt{3}$,④四边形BGDH为平行四边形.其中正确的有( )| A. | ②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
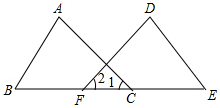 在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.