题目内容
12.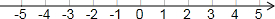 (1)计算:$\frac{2}{x+4}+\frac{{x}^{2}+4x+4}{x+4}÷\frac{{x}^{2}-4}{x-2}$
(1)计算:$\frac{2}{x+4}+\frac{{x}^{2}+4x+4}{x+4}÷\frac{{x}^{2}-4}{x-2}$(2)解不等式组$\left\{\begin{array}{l}{\frac{x+1}{3}>0,①}\\{2(x+5)≥6(x-1),②}\end{array}\right.$并将其解集在数轴上表示出来.
分析 (1)根据分式的混合计算解答即可;
(2)根据不等式组的解法解答即可.
解答 解:(1)$\frac{2}{x+4}+\frac{{x}^{2}+4x+4}{x+4}÷\frac{{x}^{2}-4}{x-2}$
=$\frac{2}{x+4}+\frac{(x+2)^{2}}{x+4}×\frac{x-2}{(x+2)(x-2)}$
=$\frac{2}{x+2}$+$\frac{x+2}{x+4}$
=1;
(2)$\left\{\begin{array}{l}{\frac{x+1}{3}>0,①}\\{2(x+5)≥6(x-1),②}\end{array}\right.$,
解不等式①可得:x>-1,
解不等式②得:x≤4,
所以不等式组的解集是:-1<x≤4,
在数轴上表示为:
点评 本题考查了分式的混合运算,因式分解、通分约分是解题的关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
20.如果把分式$\frac{5xy}{x+y}$的x与y都扩大10倍,那么这个分式的值( )
| A. | 不变 | B. | 扩大50倍 | C. | 扩大10 | D. | 缩小50倍 |
17. 如图,数轴上的点A、B、C、D、E分别对应的数是1、2、3、4、5,那么表示$\sqrt{13}$的点应在( )
如图,数轴上的点A、B、C、D、E分别对应的数是1、2、3、4、5,那么表示$\sqrt{13}$的点应在( )
 如图,数轴上的点A、B、C、D、E分别对应的数是1、2、3、4、5,那么表示$\sqrt{13}$的点应在( )
如图,数轴上的点A、B、C、D、E分别对应的数是1、2、3、4、5,那么表示$\sqrt{13}$的点应在( )| A. | 线段AB上 | B. | 线段BC上 | C. | 线段CD上 | D. | 线段DE上 |
 利用尺规、用三种不同的方法作一个三角形与已知直角三角形ABC全等,并简要说明理由.(同种理由视为是同一种方法)
利用尺规、用三种不同的方法作一个三角形与已知直角三角形ABC全等,并简要说明理由.(同种理由视为是同一种方法)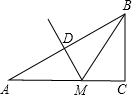 如图,△ABC中,AB的垂直平分线交AC于点M.若AC=8cm,BC=4cm,则△MBC的周长=12cm.
如图,△ABC中,AB的垂直平分线交AC于点M.若AC=8cm,BC=4cm,则△MBC的周长=12cm.